Textbook: Elements of Information

Chapter 2

熵

离散随机变量$X$的熵被定义为：

\[H(X)=-\sum p(x)\log p(x)\]

同时，他也是随机变量$\frac{1}{p(X)}$的期望值，即：$H(X)=E\log \frac{1}{p(X)}$。熵满足如下性质：

\[1. H(X)\geq 0\\ 2. H_b(X)=(\log_ba)H_a(X)\]

熵有许多意义，其中一种意义是：描述一个随机信号的最短序列的期望长度。

联合熵

一对离散随机变量$(X,Y)$的联合熵$H(X,Y)$被定义为：

\[H(X,Y)=-\sum\limits_{x\in \mathcal{X }} \sum\limits_{y\in\mathcal{Y }} p(x,y)\log p(x,y),\]

他也可以被写为$p(X,Y)$的期望。

条件熵

条件熵被定义为：

\[\begin{aligned} H(Y|X)&=\sum\limits_{x\in\mathcal{X }} p(x)H(Y|X=x)\\ &=-\sum\limits_{x\in\mathcal{X }} p(x)\sum\limits_{y\in\mathcal{Y }} p(y|x)\log p(y|x)\\ &=-\sum\limits_{x\in\mathcal{X }} \sum\limits_{y\in\mathcal{Y }} p(x,y)\log p(y|x)\\ &=-E\log p(Y|X) \end{aligned}\]

其实也是条件概率的对数的期望

链式法则

链式法则被定义为：

\[H(X,Y)=H(X)+H(Y|X)\]

证明如下：

\[\begin{aligned} H(X,Y)& =-\sum_{x\in{\mathcal X }} \sum_{y\in{\mathcal Y }} p(x,y)\log p(x,y) \\ &=-\sum_{x\in{\mathcal X }} \sum_{y\in{\mathcal Y }} p(x,y)\log p(x)p(y|x) \\ &=-\sum_{x\in\mathcal{X }} \sum_{y\in\mathcal{Y }} p(x,y)\log p(x)-\sum_{x\in\mathcal{X }} \sum_{y\in\mathcal{Y }} p(x,y)\log p(y|x) \text{,} \\ &=-\sum_{x\in\mathcal{X }} p(x)\log p(x)-\sum_{x\in\mathcal{X }} \sum_{y\in\mathcal{Y }} p(x,y)\log p(y|x) \\ &=H(X)+H(Y|X). \end{aligned}\]

还有一种简单的证明方法：

\[\log p(X,Y) = \log p(X) + \log p(Y|X)\]

还有一条：

\[H(X,Y|Z) = H(X|Z) + H(Y|X,Z)\]

相关熵和互信息

相关熵$D(p

q)$是一种度量把分布$p$假设为$q$时所带来的效率降低。即我们需要$H(p)+D(p

q)$ bits来描述一个随机变量当它是$p$我们却把它当做$q$时。相关熵的定义是：

\[\begin{aligned} D(p||q)&=\sum\limits_{x\in\mathcal{X }} p(x)\log\frac{p(x)}{q(x)}\\ &=E\log\frac{p(X)}{q(X)} \end{aligned}\]

根据此定义，如果存在一个符号$x\in\mathcal{X}$，但是$p(x)>0, q(x)=0$，则有$D(p

q)=\infty$.相关熵并不是一种两个分布之间相似度的衡量，也不满足三角不等式。

互信息$I(X,Y)$的含义是由关于另一个随机变量的知识所引起的一个随机变量的不确定度的减少。它是联合分布和成绩分布$p(x)p(y)$之间相关熵，即：

\[\begin{gathered} I\left(X;Y\right) =\sum_{x\in{\mathcal X }} \sum_{y\in{\mathcal Y }} p(x,y)\log{\frac{p(x,y)}{p(x)p(y) }} \\ =D(p(x,y)||p(x)p(y)) \\ =E_{p(x,y)}\log\frac{p(X,Y)}{p(X)p(Y)}. \end{gathered}\]

熵、互信息之间的关系

可以用这个图来表示。

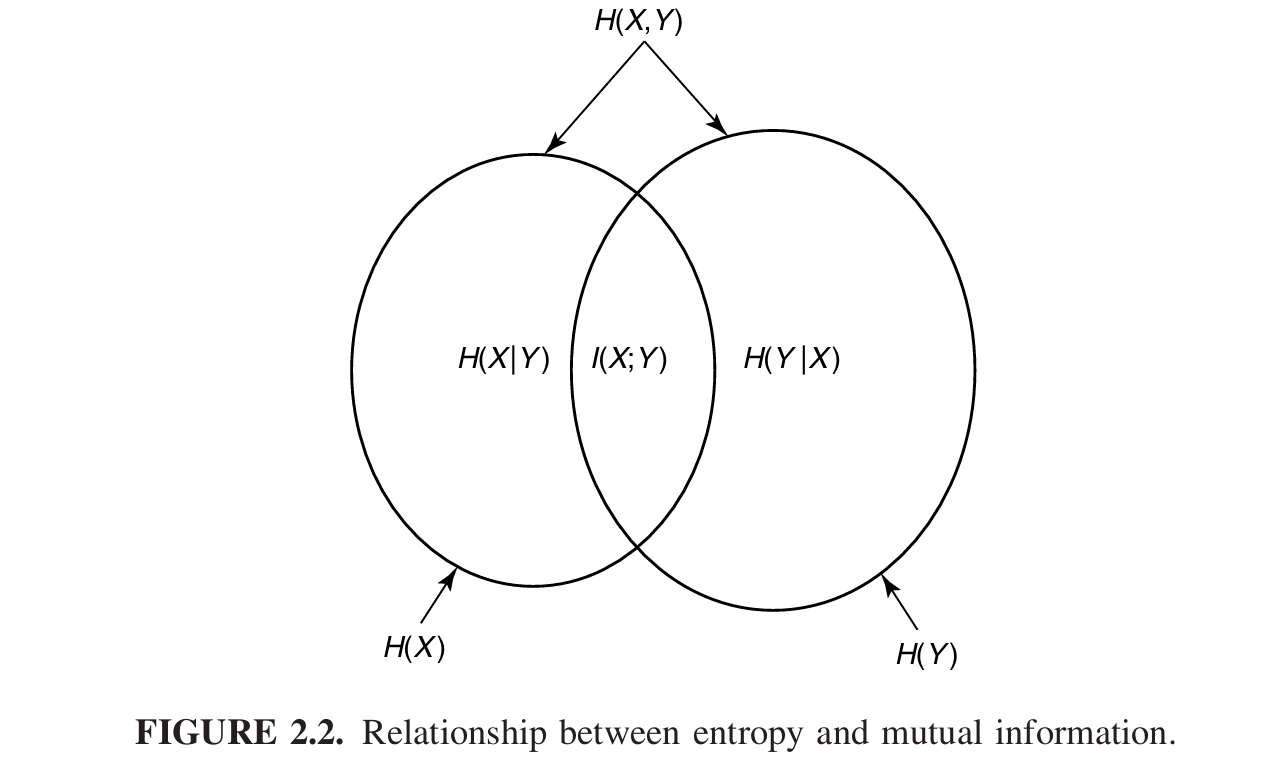
熵的链式法则

链式法则定义如下： \(H(X_1,X_2,\cdots,X_n) = \sum\limits_{i=1}^{n}H(X_i|X_{i-1},\cdots,X_1)\) 证明就重复用二元展开法则就ok

条件互信息

\(\begin{aligned} I(X;Y|Z) &= H(X|Z) - H(X|Y,Z)\\ &=E\log \frac{p(X,Y|Z)}{p(X|Z)p(Y|Z)} \end{aligned}\)

信息的链式法则

\(I(X_1,X_2,\cdots,X_n;Y) = \sum\limits_{i=1}^{n}I(X_i;Y|X_{i-1},X_{i-2},\cdots,X_1)\)

条件相关熵

对于概率密度函数$p(x,y)$和$q(x,y)$而言，条件相关熵为： \(\begin{aligned} D(p(y|x)||q(y|x)) &= \sum\limits_{x}p(x)\sum\limits_{y}p(y|x)\log \frac{p(y|x)}{q(y|x)}\\ &=E\log\frac{p(Y|X)}{q(Y|X)} \end{aligned}\)