题面

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 $n$ 个深埋在地下的宝藏屋， 也给出了这 $n$ 个宝藏屋之间可供开发的 $m$ 条道路和它们的长度。 小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远， 也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路 则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。

新开发一条道路的代价是： \(L\times K\) L代表这条道路的长度，K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋） 。 请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代 价最小，并输出这个最小值。 输入输出格式 输入格式： 第一行两个用空格分离的正整数 $n,m$，代表宝藏屋的个数和道路数。

接下来 $m$ 行，每行三个用空格分离的正整数，分别是由一条道路连接的两个宝藏 屋的编号（编号为 $1-n$），和这条道路的长度 $v$。

输出格式： 一个正整数，表示最小的总代价。

输入输出样例 输入样例# 1：

4 5 
1 2 1 
1 3 3 
1 4 1 
2 3 4 
3 4 1 

输出样例# 1：

4

输入样例# 2：

4 5 
1 2 1 
1 3 3 
1 4 1 
2 3 4 
3 4 2  

输出样例# 2：

5

样例解释

【样例解释1】 小明选定让赞助商打通了 11 号宝藏屋。小明开发了道路 $1 \to 2$，挖掘了 $2$ 号宝 藏。开发了道路 $1 \to 4$，挖掘了 $4$ 号宝藏。还开发了道路 $4 \to 3$，挖掘了 3 3号宝 藏。工程总代价为：$1 \times 1 + 1 \times 1 + 1 \times 2 = 4$ 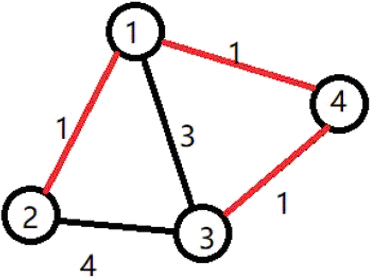【样例解释2】 小明选定让赞助商打通了 11 号宝藏屋。小明开发了道路$ 1 \to 2$，挖掘了 22 号宝 藏。开发了道路 $1 \to 3$，挖掘了 $3$ 号宝藏。还开发了道路 $1 \to 4$，挖掘了 $4$ 号宝 藏。工程总代价为：$1 \times 1 + 3 \times 1 + 1 \times 1 = 5$ 【数据规模与约定】 对于 $20\%$的数据： 保证输入是一棵树，$1 \le n \le 8，v \le 5000$ 且所有的$ v $都相等。 对于 $40\%$的数据： $1 \le n \le 8$，$0 \le m \le 1000$，$v \le 5000$ 且所有的$ v $都相等。 对于 $70\%$的数据：$ 1 \le n \le 8$，$0 \le m \le 1000$，$v \le 5000$ 对于 $100\%$的数据：$ 1 \le n \le 12$，$0 \le m \le 1000$，$v \le 50000$

解答

状压dp！？不会呀,我太弱了，dp基本就不会！怎么办啊，我要骗分啊！不骗分，怎么拿省一？？？ 此时，一种邪恶灵活的思想涌上心头——————模拟退火！万岁！那么模拟退火有两个问题需要考虑： 1.板子 2.计算新解 1板子的话，十分简单(见我另一篇题解)。如何计算新解是关键，也是对思维要求较高的退火算法思维要求已经够低了，对于这道题，我们考虑如何变化解。我们可以把这些点构造成一个序列，在序列中的位置就是它们依次被加入到结果中顺序。我们一开始把每个点的编号设为他在序列中的位置。那么我们有两种方式可以解决。1是使用STL中的random_shuffle(Iterator begin,Iterator end)函数来获得一个随机序列(因为这个数据范围只有12个点12!也q恰恰好可以卡过去，只是时间卡的有点死)。2是使用rand()随机交换两个位置的数，然后我们就可以$O(n^2)$的计算解(因为这个数据范围非常小，可以直接这样搞)，然后就是退火的老套路咯。其实不降温也可以。。。。 这里解释一下node里面的dis函数的计算原理，就是随机获得一个序列以后，把这个序列看做每个点加到结果里面的顺序，然后找一个点，使当前计算的点连接到那个点产生的价格最小。别忘了把dep更新！！！

# include <cstdio>
# include <cstring>
# include <cstdlib>
# include <cmath>
# include <ctime>
# include <algorithm>
using namespace std;
const int INF = 999999999;
int n,m,q;
int read(){
	int x = 0,f = 1;static char c = getchar();
	while(c<'0'||c>'9'){if(c=='-')f = -1;c = getchar();}
	while(c>='0'&&c<='9'){x = (x<<1)+(x<<3)+c-'0';c = getchar();}
 	return x*f;
}
const int MAXN = 13;
int map[MAXN][MAXN];
struct node{
	int d[MAXN];int dep[MAXN];
	node(){
		for(int i = 1;i<=n;i++)d[i] = i,dep[i] = 0;
	}
	node (node &n2){
		memcpy(n2.d,d,sizeof(d));memset(dep,0,sizeof(dep));
		swap(d[rand()%n+1],d[rand()%n+1]);
	}
	int dis(){
		dep[1] = 1;
		int ans;
		for(int i = 2;i<=n;i++){
			int temp = INF;
			for(int j = 1;j<i;j++){
				if(map[d[j]][d[i]]!=0x3f3f3f3f&&map[d[j]][d[i]]*dep[j]<temp){
					temp = map[d[j]][d[i]]*dep[j];
				}
			}
			if(temp == INF){
				return temp;
			}else ans+=temp;
		}
		return ans;
	}
};
const double T = 19260817;
const double delta = 0.997;
node current_ans;
int SA(){
	double curr_T = T;
	while(T>0.01){
		node new_ans(current_ans);
		int del = new_ans.dis()-current_ans.dis();
		if(del<0){
			current_ans = new_ans;
		}else if(exp(-del/curr_T)*RAND_MAX>rand()){
			current_ans = new_ans;
		}
		curr_T*=delta;
	}
}
int main(){
	n = read();
	m = read();
	int f,t,w;
	for(int i = 1;i<=m;i++){
		f = read(),t = read(),w = read();
		map[f][t] = map[t][f] = w;
	}
	int ans = 999999999;
	while((double)clock()/(double)CLOCKS_PER_SEC<0.9){
		ans = min(ans,SA());
	}
	printf("%d",ans);
    return 0;
}