树形dp
普通树形dp
其实就是没有上司的舞会,比较简单
背包类树形dp
例如选课,其实就是一个分组背包问题和树形dp结合起来。$F[x][t]$表示以$x$为根的子树中选$t$门课能够获取的最高学分。下面是一个非常搞扯的表达式,反正自己意会就行 \(F[x][t] = max_{\sum^p_{i=1}c_i=t-1}\{\sum^p_{i=1}F[y_i,c_i]+score[x]\}\) 以下是实现的代码。
# include <iostream>
using namespace std;
const int MAXN = 310;
const int MAXM = 310;
int indegree[MAXN];
struct edge{
int t,w,next;
}edges[MAXN];
int head[MAXN];
int top;
void add(int f,int t,int w) {
edges[++top].next = head[f];
edges[top].t = t;
edges[top].w = w;
// indegree[t]++;
head[f] = top;
}
int score[MAXN];
int F[MAXN][MAXM];
int n,m;
void dfs(int x){
for(int i = head[x];i!=0; i = edges[i].next){
int t = edges[i].t;
dfs(t);
for(int j = m;j>=0;j--){//为了处理组内选取0个课程的情况
for(int k = j;k>=0;k--){
if(j-k>=0){
F[x][j] = max(F[x][j],F[x][j-k]+F[t][k]);
}
}
}
}
if(x!=0){
for(int i = m;i>0;i--)F[x][i] = F[x][i-1]+score[x];
}
}
int main(void){
cin>>n>>m;
int si,ki;
for(int i = 1;i<=n;i++){
cin>>si>>ki;
score[i] = ki;
add(si,i,ki);
}
dfs(0);
cout<<F[0][m];
return 0;
}
状态压缩DP
解答
其实是一道状压dp的裸题!
我们以当前扩展到了第$i$行作为状态,然后用1表示竖着的矩形的上面的一个0表示其他情况
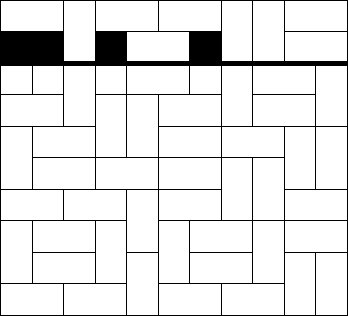 那么怎么转移呢?
设$F[i,j]$为第$i$行为$j$状态的时候的分割总数。j是用十进制记录的$M$位的二进制数。
第$i-1$行的形态$k$能够转移到$j$时,当且仅当:
那么怎么转移呢?
设$F[i,j]$为第$i$行为$j$状态的时候的分割总数。j是用十进制记录的$M$位的二进制数。
第$i-1$行的形态$k$能够转移到$j$时,当且仅当:
- $j$和$k$的
按位与运算的结果为$0$。这保证了每个数字$1$的下方必须是$0$,代表补全竖着的$1\times 2$的长方形 - $j$和$k$执行按位或运算的结果的二进制表示中,每一段连续的$0$都必须有偶数个 这些0代表若干个横着的$1\times 2$长方形,奇数个$0$无法分割成这种形态
我们需要预处理出$[0,2^M-1]$内所有满足“每一段连续的$0$都必须有偶数个”的整数,记录在集合S中 方程:\(F[i,j] = \sum_{j\&k=0并且j|k\in S}F[i-1,k]\) 然后dp的初始值:F[0,0] = 1,其余为0 目标:F[N,0] 复杂度$O(2^M2^MN) = O(4^MN)$ 注意,打出来的数非常大,需要用long long code:
# include <cstdio>
# include <iostream>
using namespace std;
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
int F[12][1<<11];
bool canGo[1<<11];
int main(){
int n,m;
while(cin>>n>>m&&n){
for(int i = 0;i<1<<m;i++){
bool cnt = 0,has_odd = 0;
for(int j = 0;j<m;j++){
if(i>>j&1)has_odd|=cnt,cnt = 0;
else cnt^=1;
}
canGo[i] = has_odd|cnt?0:1;
}
F[0][0] = 1;
for(int i = 1;i<=n;i++){
for(int j = 0;j<1<<m;j++){//遍历每个状态
F[i][j] = 0;
for(int k = 0;k<1<<m;k++){//便利可以转移的状态
if((j&k)==0&&canGo[j|k])F[i][j]+=F[i-1][k];
}
}
}
cout<<F[n][0]<<endl;
}
return 0;
}
倍增优化
过两天学
数据结构优化DP
过两天学
单调队列优化DP
其实就是用一个单调队列存储可能的状态集合,这样遍历的时候就不需要遍历所有已知的状态了,因为有些状态是明显不可能成立的。适用于形如以下形式的dp\(F[x] = \underset{k\in [x-m,x-1]}{max/min}(F[k])+val[x]\) 照例一道例题:poj1821
解答
首先设计状态,我们用$F[i,j]$表示前$i$个工人粉刷前j个木板的最大收益,那么如何转移呢?
- 第$i$个工匠可以什么也不刷,此时$F[i][j]=F[i-1,j]$
- 第$j$块木板可以空着不刷,此时$F[i][j] = F[i][j-1]$
- 第$i$个工匠粉刷第$K+1$到第$j$块木板。由题意,该工匠粉刷总数不能超过$Li$,且必须粉刷$Si$,所以需要满足:$k+1\leq S_i\leq Li$并且$j-k\leq Li$于是乎就有\(F[i,j] = \underset{j-Li\leq k\leq Si-1}{max}{F[i-1,k]+Pi*(j-k)}其中j\geq Si\)
如何优化呢?不难发现如下规律
- P_i *j除定值$i$外,只有状态变量$j$
- F[i-1,k]-p_i*k除$i$以外,只有决策变量$k$
那么状态转移方程可以转移为\(F[i,j] = \underset{j-Li\leq k\leq Si-1}{max}{F[i-1,k]-Pi*k}+Pi*j其中j\geq Si\) 然后就可以用上单调队列优化的dp了。 我们发现对于$k_1$和$k_2$如果k1比k2更靠后,那么随着j的增长,k2会比k1更先被淘汰,并且,如果k1和k2满足\(F[i-1,k1]-pi*k1\geq F[i-1,k2]-pi*k2\)那么就意味着,k2永远不会成为最优解,那么直接排除候选集合。综上,我们只需要维护一个决策点k单调递增,数值$F[i-1,k]-Pi*k$单调递减的队列。只有这个队列中的决策才有可能在某一时刻成为最优决策。这个队列满足以下条件:
- 当j变大时,检查队头元素,把小于$j-Li$的决策出队
- 查询最优解时,队头就是所求
- 有一个新的决策要加入集合时,在队尾检查$F[i-1,k]-Pi*k$的单调性,把无用决策从队尾直接出队,最后把新决策加入队尾。
那么对于这道题,从内层循环开始时(j=Si),建立一个空的单调队列,把$[max(S_i-L_i,0),S_i-1]$中的决策依次加入候选集合,对于每个$j=Si~N$,先在队头检查决策合法性,然后取队头为最优决策进行状态转移。每个决策入队出队依次,转移复杂度$O(1)$总体复杂度$O(MN)$ 代码:
//
// Created by dhy on 18-12-22.
//
# include <cstring>
# include <iostream>
# include <deque>
# include <algorithm>
using namespace std;
struct worker{int si,li,pi;}workers[110];
bool operator<(const worker &w1,const worker &w2){return w1.si<w2.si;}
int F[110][16010];
int cal(int i,int k){//前面提到过的小优化,方便计算
return F[i-1][k]-workers[i].pi*k;
}
int n,m;
int main() {
cin>>n>>m;
for(int i = 1;i<=m;i++)cin>>workers[i].li>>workers[i].pi>>workers[i].si;
sort(workers+1,workers+m+1);//按Si从大到小排序,这样就可以愉快地按线性dp的方式来啦
for(int i = 1;i<=m;i++){
deque<int> q;//这里我采用双端队列,方便维护这个单调队列
for(int k = max(0,workers[i].si-workers[i].li);k <= workers[i].si-1;k++){
//int k = max(0,workers[i].si-workers[i].li)是为了强制包含si,然后枚举从si
之前的哪个木板开始刷(题目说了是连续的)
//k <= workers[i].si-1是为了防止把si这一块刷2次
while(!q.empty()&&cal(i,q.back())<=cal(i,k))q.pop_back();//排除队列里面根本不可能出现在决策的集合
q.push_back(k);//把当且决策加入集合
}
for(int j = 1;j<=n;j++){//开始枚举每一块木板
F[i][j] = max(F[i-1][j],F[i][j-1]);//不粉刷时的转移
if(j>=workers[i].si){//粉刷k+1~j块木板的转移
while(!q.empty()&&q.front()<j-workers[i].li)q.pop_front();//排除不合法的决策
if(!q.empty())F[i][j] = max(F[i][j],cal(i,q.front())+workers[i].pi*j);//队列飞控时,取队头进行状态转移
}
}
}
cout<<F[m][n]<<endl;
return 0;
}
思考题:poj3017 寒假再来做吧 单调队列优化的多重背包多重背包dp方程\(F[i] = max(F[i],F[i-k*v]+k*w)\) 然后我们把i-kv改写一下。把i看做是u+pv的形式,其中u是状态i按照对vi的取模进行分类的。然后这样以后dp方程就转化为了\(F[u+p*vi] = \underset{p-Ci\leq k \leq p-1}{max} \{F[u+k*vi]+(p-k)*wi\}\)这样就可以把倒序循环j的过程改为对于每个余数$u\in [0,vi-1]$,倒序循环$p = \lfloor(M-u)/Vi~0$M是背包容量,对应状态就是$j = u+p*vi$.第i个物品只有Ci个,故能转移到j = u = p * vi的决策候选集合就是$\{u+k*Vi|p-Ci\leq k \leq p-1\}$。然后与fence那道题一样,把外层循环i 和 u 看成定值,当内层循环变量p减小1时,决策k取值范围$[p-Ci,p-1]$的上下界统统缩小。状态转移方程等号右侧的式子依然分为两部分,仅包含变量p的p*wi和仅包含k的$F[u+k*vi]-k*wi$那么,我们只需要维护一个k单调递增,$F[u+k*vi]-k*wi$单调递减的队列。三个管理操作:
- 检查队头合法性,把大于p-1的决策点出队
- 取队头为最优策略,更新$F[u+p*vi]$
- 把新决策$k = p-Ci-1$插入队尾,入队前检查单调性,排除无用决策。
整个算法复杂度$O(MN)$
//
// Created by dhy on 18-12-23.
//
# include <cstring>
# include <cstdio>
# include <deque>
using namespace std;
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
const int MAXN = 1e6;
const int MAXM = 1e6;
int F[MAXM];
int V[MAXN];
int C[MAXN];
int W[MAXN];
inline int cal(int i,int u,int k){return F[u+k*V[i]]-k*W[i];}
int n,m;
int main() {
n = read(),m = read();
memset(F,0xcf, sizeof(F));//-INF
F[0] = 0;
for(int i = 1;i<=n;i++){
V[i] = read(),W[i] = read(),C[i] =read();
for(int u = 0;u<V[i];u++){
deque<int> q;
int maxp = (m-u)/V[i];
for(int k = maxp-1;k>=max(maxp-C[i],0);k--){//初始化状态这里,为什么是maxp-1我再去问问
while(!q.empty()&&cal(i,u,q.back())<=cal(i,u,k))q.pop_back();
q.push_back(k);
}//倒叙循环每个状态
for(int p = maxp;p>=0;p--){
while(!q.empty()&&q.front()>p-1)q.pop_front();//删除违法状态
if(!q.empty())F[u+p*V[i]] = max(F[u+p*V[i]],cal(i,u,q.front())+p*W[i]);//计算新解
if(p-C[i]-1>=0){//插入新决策,同时维护单调性
while(!q.empty()&&cal(i,u,q.back())<=cal(i,u,p-C[i]-1))q.pop_back();
q.push_back(p - C[i] - 1);
}
}
}
}
int ans = 0;
for(int i = 1;i<=n;i++)ans = max(ans,F[i]);
printf("%d ",ans);
return 0;
}
