![P2704 [NOI2001]炮兵阵地](/images/posts/OI.png)
题面
司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：
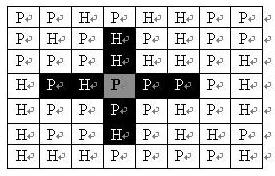
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入输出格式
输入格式：
第一行包含两个由空格分割开的正整数，分别表示N和M；
接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。
输出格式：
仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。
输入输出样例
输入样例# 1：
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例# 1：
6
解答
注意强调一下main读入地图的时候m必须从0开始.
首先我们考虑状态。我们不难想到状压dp套路以第$i$行，当前行的状态压缩过后在集合S*为$j$的编号的状态，上一行为编号为$k$的状态作为整个题的状态。可以写出如下递推式:(count(x)表示x的二进制表示下有多少个1)
\(dp[i][j][k] = max(dp[i-1][k][l]+count(j)) \ \ \ \ \ 如果这个状态可行的话\)
那么什么状态是可行的呢？首先我们要考虑$i-2$行，当行前状态$j$与$i-1$行状态$k$与$i-2$行的状态$l$要满足\(j\&k=0\ \ j\&l=0 \ \ \ k\&l = 0\)
当然了，还有最重要的一点那就是整个地图，我们同样压位压到二进制数里面，只需要在状态转移以前判断这个状态可不可行就行。
前文所说的集合S，其实表示的是可行的状态的集合。什么意思呢？我们发现如果一个地方放炮兵，那么左右两格之内都不能放炮兵。也就是说，二进制状态压缩以后，一位为1，那么它左右两位都必须为0。我们就只需要把这个集合提前算出来，极大简化了复杂度，因为这个集合并不大！
那么，这道题就算完了，总复杂度$O(n|S|^3)$,由于$|S|$很小，所以整个算法表现非常优秀
//
// Created by dhy on 18-12-16.
//
# include <cstring>
# include <iostream>
using namespace std;
int dp[110][77][77];
int S[100];
int map[101];
int cnt[101];
int top;
int n,m;
int getBit(int x){
int c = 0;
while(x)c++,x-=x&-x;
return c;
}
bool ok(int x){
if(x&(x<<1))return false;
if(x&(x<<2))return false;
return true;
}
void init(){
int end = 1<<m;
for(int i = 0;i<end;i++)if(ok(i))S[top] = i,cnt[top++] = getBit(i);
}
bool valid(int l,int x){
if(map[l]&x)return false;
return true;
}
inline int max(int a,int b){return a>b?a:b;}
int work(){
memset(dp,-1, sizeof(dp));
dp[0][0][0] = 0;
int ans = 0;
for(int i = 0;i<top;i++){
if(valid(1,S[i])){
dp[1][i][0] = cnt[i];
ans = max(ans,dp[1][i][0]);
}
}
for(int i = 2;i<=n;i++){
for(int j = 0;j<top;j++){
if(valid(i,S[j]))
for(int k = 0;k<top;k++){//i-1
if(valid(i-1,S[k])&&(S[j]&S[k])==0){
int last = 0;
for(int l = 0;l<top;l++){//i-2
if(dp[i-1][k][l]!=-1&&(S[l]&S[j])==0&&valid(i-2,S[l])){
last = max(last,dp[i-1][k][l]);
}
}
dp[i][j][k] = max(dp[i][j][k],last+cnt[j]);
if(i==n)ans = max(ans,dp[i][j][k]);
}
}
}
}
return ans;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++){
for (int j = 0; j < m; j++) {
char t;
cin >> t;
if (t == 'H')map[i] |= (1 << (m - 1 - j));
}
}
init();
cout<<work()<<endl;
return 0;
}
