题面
有一个ab的整数组成的矩阵,现请你从中找出一个nn的正方形区域,使得该区域所有数中的最大值和最小值 的差最小。
输入
第一行为3个整数,分别表示a,b,n的值第二行至第a+1行每行为b个非负整数,表示矩阵中相应位置上的数。每 行相邻两数之间用一空格分隔。 100%的数据2<=a,b<=1000,n<=a,n<=b,n<=100
输出
仅一个整数,为ab矩阵中所有“nn正方形区域中的最大整数和最小整数的差值”的最小值。
样例输入
5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2
样例输出
1
提示
问题规模 (1)矩阵中的所有数都不超过1,000,000,000
(2)20%的数据2<=a,b<=100,n<=a,n<=b,n<=10
(3)100%的数据2<=a,b<=1000,n<=a,n<=b,n<=100
解答
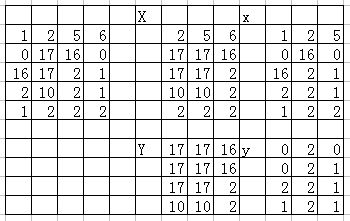
先用单调队列处理每一行,用$X[i][j]$表示第$i$行,以$j$列开始,长度为$n$的$1\times n$的矩形的最大值。用$x[i][j]$表示第$i$行,以$j$列开始,长度为$n$的$1\times n$的矩形的最小值这样每一行都处理一下。这样以后,再竖着来对$X$和$x$做,就可以做出每一个方块的最大最小值,然后暴力枚举,好了。解释如下图
 代码:
代码:
# include <cstdio>
# include <iostream>
# include <queue>
# include <algorithm>
# include <stdio.h>
# include <deque>
# include <cstring>
# define LL long long
using namespace std;
const int MAXN = 1010;
long long map[MAXN][MAXN];
long long x[MAXN][MAXN],X[MAXN][MAXN];
long long y[MAXN][MAXN],Y[MAXN][MAXN];
int a,b,n;
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
int main(){
ios::sync_with_stdio(false);
cin>>a>>b>>n;
for(int i = 1;i<=a;i++)for(int j = 1;j<=b;j++)cin>>map[i][j];
for(int i = 1;i<=a;i++){
deque<long long> Q,q;
Q.push_back(1),q.push_back(1);
for(int j = 2;j<=b;j++){
while(!q.empty()&&map[i][j]<=map[i][q.back()])q.pop_back();
q.push_back(j);
while(!Q.empty()&&map[i][j]>=map[i][Q.back()])Q.pop_back();
Q.push_back(j);
while(q.front()<=j-n)q.pop_front();
while(Q.front()<=j-n)Q.pop_front();
if(j>=n){X[i][j-n+1] = map[i][Q.front()],x[i][j-n+1] = map[i][q.front()];}
}
}
for(int i = 1;i<=b-n+1;i++){
deque<long long> Q,q;
Q.push_back(1),q.push_back(1);
for(int j = 2;j<=a;j++){
while(!Q.empty()&&X[j][i]>=X[Q.back()][i])Q.pop_back();
Q.push_back(j);
while(!q.empty()&&x[j][i]<=x[q.back()][i])q.pop_back();
q.push_back(j);
while(Q.front()<=j-n)Q.pop_front();
while(q.front()<=j-n)q.pop_front();
if(j>=n){Y[j-n+1][i] = X[Q.front()][i]; y[j-n+1][i] = x[q.front()][i];}
}
}
long long ans = 0x7f7f7f77f7f7f7;
for(int i = 1;i<=a-n+1;i++)for(int j = 1;j<=b-n+1;j++)ans = min(ans,Y[i][j]-y[i][j]);
cout<<ans;
return 0;
}
