求法
1.tarjan 的离线求法,用并查集维护。不多赘述 2.欧拉序:
树的欧拉序是对树进行DFS的一种序列。有两种形式: 1、在每个结点进和出都加进序列。 2、只要到达每一个结点就把他加进序列。
eg:
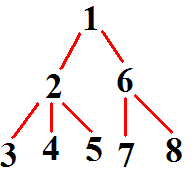 欧拉序为:1 2 3 2 4 2 5 2 1 6 7 6 8
欧拉序为:1 2 3 2 4 2 5 2 1 6 7 6 8
基于RMQ问题的处理法: 1.对树dfs,算出每个节点的dfs序first[i],每个 节点的深度dep[i] • 2.对dfs序做区间最小值预处理。 • 3.根据dfs序预处理出区间最小值RMQ查询 表 • 4.然后就可以查询了
倍增求法
思想:求出每个点深度,把更深的向上 跳成深度一致,然后一个点一个点向上 跳, 跳到了一个点上就是最近公共祖先。这 样太慢,就有了倍增法 算法步骤
1.对树dfs,算出每个节点的父亲,深度 2.计算出每个点的第2^j祖先是谁 3.查询
eg:woj2723 代码如下:
# include <cstdio>
# include <algorithm>
using namespace std;
const int MAXN = 100010;
struct edge{int t,f,w,next;bool operator<(const edge &e2)const {return w<e2.w; }} edges[MAXN<<1];
int head[MAXN],top;
int father[MAXN][25];
int wei[MAXN][25];
int dep[MAXN];
int n ,m;
bool vis[MAXN];
int fa[MAXN];
edge edges2[MAXN];
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
inline bool judge(int x,int y){return find(x)==find(y);}
inline void unionn(int x,int y){fa[find(y)]=find(x);}
inline void swap(int &x,int &y){x = x^y;y = y^x;x= x^y;}
void add(int f,int t,int w){
edges[++top].next = head[f];
edges[top].t = t;
edges[top].w = w;
head[f] = top;
}
void kruskal(){
sort(edges2+1,edges2+1+m);
int cnt = 0;
for(int i = 1;i<=m;i++){
if(!judge(edges2[i].f,edges2[i].t)){
unionn(edges2[i].f,edges2[i].t);
cnt++;
add(edges2[i].f,edges2[i].t,edges2[i].w);
add(edges2[i].t,edges2[i].f,edges2[i].w);
}
if(cnt==n-1)return;
}
}
void dfs(int fa,int x){
vis[x] = true;dep[x] = dep[fa]+1;
father[x][0] = fa;
for(int i = head[x];i;i = edges[i].next){
int t = edges[i].t;
if(!vis[t]){
wei[t][0] = edges[i].w;
dfs(x,t);
}
}
}
void initLCA(){
for(int i = 1;i<=n;i++)if(!vis[i])dfs(0,i);
for(int i = 1;i<=24;i++){
for(int j = 1;j<=n;j++){
father[j][i] = father[father[j][i-1]][i-1];
wei[j][i] = max(wei[j][i-1],wei[father[j][i-1]][i-1]);
}
}
}
int LCA(int x,int y){
if(dep[x]<dep[y])swap(x,y);
int ans = 0;
int delta = dep[x]-dep[y];
for(int i = 0;i<=24;i++){
if(delta&(1<<i)){
ans = max(wei[x][i],ans);
x = father[x][i];
}
}
if(x==y)return ans;
for(int i = 24;i>=0;i--){
if(father[x][i]!= father[y][i]){
ans = max(wei[x][i],ans);
ans = max(wei[y][i],ans);
x = father[x][i], y =father[y][i];
}
}
ans = max(wei[x][0],ans);
ans = max(wei[y][0],ans);
return ans;
}
int main(){
n = read(),m = read();
for(int i = 1;i<=m;i++){
int f = read(),t = read(),w = read();
edges2[i].f = f,edges2[i].t = t,edges2[i].w = w;
}
for(int i = 1;i<=n;i++)fa[i] = i;
kruskal();
initLCA();
int Q = read();
while(Q--){
int f = read(),t = read();
printf("%d\n",LCA(f,t));
}
return 0;
}
注意LCA函数里面那个 if(x==y)return ans;很重要
一个有用的拓展:
多个点的LCA查询
解法
结论:多个点的LCA就是其中dfs序最小和最大的LCA
补充
欧拉序求LCA:
求某两点的LCA。显然这两点之间的区间中,深度最小点就是LCA。这可以用RMQ解决。
求某个子树的权值和,方法是:只记录第一次出现的数的值,同样的查询某点就只需要查询该点在欧拉序中最后出现的位置的前缀即可减去第一次出现的额位置-1的前缀和即可。
换根操作:这种欧拉序相当于以根为起点围着树跑了一圈,那么我们就可以把欧拉序写成一个环就是:
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6
以某个点为跟的欧拉序就是以某个点在上面的欧拉序中第一次出现的位置为起点向前走(2*n-1)步,例如以4为根的欧拉序就是
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6
