主席树
eg1 :第k大的数woj 1903
题意：n个数，m次查询，查询任意区间第k大。
首先我们发现这个题满足区间减法。如果[1,l-1]中有k个比x小的数，[1,r]中有k2个比x小的数，那么[l,r]中一共有k2-k个数比x小。基本思想就是我们做n个权值线段树，然后树相减。什么情况下可以相减呢？他们必须是同构的(就是长得一样).抄几张图
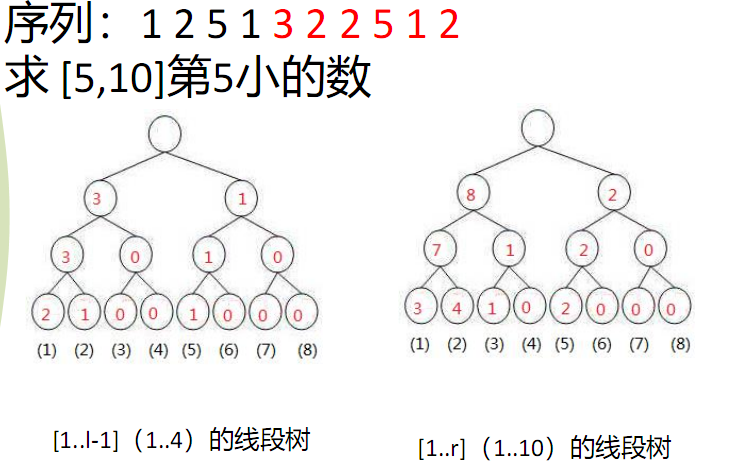
但是直接建立n颗树的话会炸空间，于是乎只好利用历史信息来做了。如下图
以下是抄的代码(回去有空写自己的代码)
# include <iostream>
# include <algorithm>
using namespace std;
const int MAXN = 1e5+5;
int L[MAXN<<5],R[MAXN<<5],sum[MAXN<<5];
int top;
int a[MAXN],tree[MAXN],HASH[MAXN];
int build(int l,int r){
int root = ++top;
sum[root] = 0;
int mid = l+r>>1;
if(l<r){
L[root] = build(l,mid);
R[root] = build(mid+1,r);
}
return root;
}
int update(int pre,int l,int r,int x){
int root = ++top;
L[root] = L[pre],R[root] = R[pre];
sum[root] = sum[pre]+1;
if(l<r){
int mid = l+r>>1;
if(x<=mid)
L[root] = update(L[pre],l,mid,x);
else R[root] = update(R[pre],mid+1,r,x);
}
return root;
}
int query(int k,int f,int t,int l,int r){
if(l>=r){
return l;
}
int mid = l+r>>1;
int num = sum[L[t]]-sum[L[f]];
if(num>=k){
return query(k,L[f],L[t],l,mid);
}else{
return query(k-num,R[f],R[t],mid+1,r);
}
}
int main(){
ios::sync_with_stdio(false);
int n,m;cin>>n>>m;
for(int i = 1;i<=n;i++){
cin>>a[i];HASH[i] = a[i];
}
sort(HASH+1,HASH+n+1);
int d = unique(HASH+1,HASH+n+1)-HASH-1;
tree[0] = build(1,d);//先建颗树
for(int i = 1;i<=n;i++){
int x = lower_bound(HASH+1,HASH+1+d,a[i])-HASH;
tree[i] = update(tree[i-1],1,d,x);//更新
}
int l,r,k;
while(m--){
cin>>l>>r>>k;
int x = query(k,tree[l-1],tree[r],1,d);//同构树相减
cout<<HASH[x]<<endl;
}
}
