试题地址：njfls的一套NOIP模拟
T1
大水模拟题，但是要用到一下结论 $\sum\limits_{i=0}^{\infty}d^i = \frac{1}{1-d}(0<d<1)$
说白了就是等比数列求和公式趋近于正无穷的情况。虽然我还是谢了模拟
代码：
# include <iostream>
# include <cstring>
# include <cstdio>
# include <cmath>
using namespace std;
const double eps = 1e-6;
const double PI = acos(-1);
double theta,v,d,g;
void file(){
freopen("physics.in","r",stdin);
freopen("physics.out","w",stdout);
}
double work(){
double ans = 0.0;
double SIN = sin(PI*theta/180);
double COS = cos(PI*theta/180.0);
while(v>eps){
double t = v*SIN/g*2.0;
ans += v*COS*t;
v*=d;
}
return ans;
}
int main(){
file();
int T;scanf("%d",&T);
while(T--){
scanf("%lf%lf%lf%lf",&theta,&v,&d,&g);
if(fabs(d)<eps){
double t = v*sin(PI*theta/180.0)/g*2.0;
printf("%.5lf\n",t*v*cos(PI*theta/180.0));
}else{
printf("%.5lf\n",work());
}
}
return 0;
}
T2
最难的一道题。首先我们可以考虑可以把成倍数关系的数放到一条链上面如下图所示
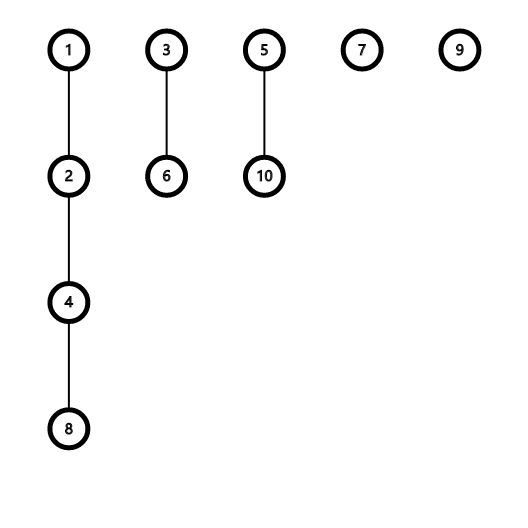然后我们发现对于一条长度不为1的链，其实就是个类似于二分图的东西，于是乎它的贡献就是2，对于所有长度不为1的链的总贡献就是$2^c$现在考虑单独的点，既可以在A也可以在B，我们不妨记所有长度不为1的链的点的个数为$sum$，那么我们的答案就是\(s^c\times {sum-n \choose m-\frac{c}{2 }}\).难点就在于如何计算长度不为1的链的条数，有一种做法是$O(n)$的枚举，但是显然过不了所有的点的，所以我们考虑log级别的算法，我们发现链长都是$2^k$的长度的，可以考虑枚举这个$k$,然后计算这个长度内所有的点数就好了,计算的时候注意代码细节。然后由于数量很大，所以需要使用lucas定理进行计算组合数。
代码：(有大量代码细节！！！)
# include <iostream>
# include <cstring>
# include <cstdio>
# define int long long
using namespace std;
const int MAXN = 10000020;
const int mod = 10000019;
int add(int a,int b){return a+b>=mod?a+b-mod:a+b;}
int sub(int a,int b){return a-b<0?a-b+mod:a-b;}
int mul(int a,int b){return 1LL*a*b%mod;}
int fac[MAXN],rev[MAXN];
long long n,sum,A,q,tmp=1;
int fp(int b,int p){
int ans = 1;
while(p){
if(p&1)ans = ans*b%mod;
b = b*b%mod;
p>>=1;
}
return ans;
}
void init(){
fac[0] = 1;fac[1] = 1;
for(int i = 2;i<mod;i++)fac[i] = 1ll*fac[i-1]*i%mod;
rev[mod-1] = fp(fac[mod-1],mod-2);
for(int i = mod-2;i>=0;i--)rev[i] = 1ll*(rev[i+1]*(i+1))%mod;
}
inline int C(int n,int m){
if(n>m)return 0;
return mul(mul(fac[m],rev[n]),rev[m-n]);
}
inline int lucas(long long n,long long m){
if(!n)return 1;
return mul(C(n%mod,m%mod),lucas(n/mod,m/mod));
}
int calc(long long l,long long r){
return (r-l+1)/2+((l&1)&&(r&1));
}
int query(int x){
if(x<A||x>A+sum)return 0;
return mul(tmp,lucas(x-A,sum));
}
signed main(){
init();
scanf("%lld%lld",&n,&q);
for(int i = 1;(1ll<<(i-1))<=n;i++){
long long l = n/(1ll<<i)+1,r = n/(1ll<<(i-1)),num = calc(l,r);
A+=(i/2ll)*num;
(i&1ll)?sum+=num:tmp = mul(tmp,fp(2,num%(mod-1)));
}
long long x;
while(q--){
scanf("%lld",&x);
printf("%lld\n",query(x));
}
return 0;
}
T3
写挂了的线段树分治的板子题。艹我真的太菜了，什么都可以写挂，一个并查集写挂了，顺带把留给T2的时间也耗完了 代码:
# include <iostream>
# include <cstring>
# include <cstdio>
# include <vector>
# include <map>
# define clear(x) memset(x,0,sizeof(x))
# define int long long
//艹全局long long
using namespace std;
const int MAXN = 200010;
const int mod = 1000000007;
int n,m;
void file(){
freopen("geography.in","r",stdin);
freopen("geography.out","w",stdout);
}
struct Q{int f,t;
Q(int f,int t):f(f),t(t){}
Q(){}
}qs[MAXN];int qcnt;
struct opt{
int op,f,t;
opt(int op,int f,int t):op(op),f(f),t(t){}
opt(){}
}ops[MAXN];int op_cnt;
int re[MAXN];
struct node{int x,sze;}stk[MAXN];int stop;
int fa[MAXN],sze[MAXN];
int find(int x){return fa[x]==x?x:find(fa[x]);}
void unite(int x,int y){
int fx = find(x),fy = find(y);
if(fx==fy)return;
if(sze[fx]<sze[fy])swap(fx,fy);
fa[fy] = fx;
stk[++stop] = node{fy,sze[fy]};
stk[++stop] = node{fx,sze[fx]};
sze[fx] = sze[fx]+sze[fy];
}
void undo(int curr){
while(stop>curr){
node pre = stk[stop--];
fa[pre.x] = pre.x;
sze[pre.x] = pre.sze;
}
}
vector<int> tree[MAXN<<2];
void modify(int k,int l,int r,int x,int y,int id){
if(l>=x&&r<=y)return (void)tree[k].push_back(id);
int mid = l+r>>1;
if(x<=mid)modify(k<<1,l,mid,x,y,id);
if(y>mid)modify(k<<1|1,mid+1,r,x,y,id);
}
int rev(int x){
return re[x];
}
int ans = 1;
int res[MAXN];
void dfs(int k,int l,int r){
int curr = stop,cur_ans = ans;
for(int i = 0;i<tree[k].size();i++){
int f = qs[tree[k][i]].f,t = qs[tree[k][i]].t;
int fx = find(f),fy = find(t);
if(fx==fy)continue;
ans = ans*(sze[fx]+sze[fy])%mod;
ans = (ans*rev(sze[fx]))%mod;
ans = (ans*rev(sze[fy]))%mod;
ans%=mod;
unite(fx,fy);
}
if(l==r){
res[l] = ans;
undo(curr);ans = cur_ans;
return;
}
int mid = l+r>>1;
dfs(k<<1,l,mid);dfs(k<<1|1,mid+1,r);
undo(curr);ans = cur_ans;
}
map<pair<int,int> ,int> tme;
bool exid[MAXN];
pair<int,int> ps[MAXN];
signed main(){
scanf("%lld%lld",&n,&m);
for(int i = 1;i<=n;i++)fa[i] = i,sze[i] = 1;
int op,f,t;
re[1] = 1;
for(int i = 2;i<=n;i++)re[i] = (mod-mod/i)*re[mod%i]%mod;
for(int i = 1;i<=m;i++){
scanf("%lld%lld%lld",&op,&f,&t);
ops[i] = opt(op,f,t);
}
for(int i = 1;i<=m;i++){
op = ops[i].op,f= ops[i].f,t = ops[i].t;
if(op==1){
ps[i] = make_pair(f,t);
tme[make_pair(f,t)] = i;
}else{
ps[i] = make_pair(f,t);
qs[++qcnt] = Q(f,t);
int st = tme[make_pair(f,t)];
modify(1,1,m,st,i-1,qcnt);
tme[make_pair(f,t)] = 0;
}
}
for(int i = 1;i<=m;i++){
if(tme[make_pair(ops[i].f,ops[i].t)]){
qs[++qcnt] = Q(ops[i].f,ops[i].t);
modify(1,1,m,tme[make_pair(ops[i].f,ops[i].t)],m,qcnt);
}
}
dfs(1,1,m);
for(int i = 1;i<=m;i++)printf("%d\n",res[i]);
return 0;
}
