Floyed

O($n^3$) 步骤 1.初始化，点U，V相连则dis[u][v] = w[u][v] 若不相连则dis[u][v] = 0x7FFFFFF; 2.

for(int k = 1;k<=n;k++)//中专点放第一个
    for(int i = 1;i<=n;i++)
        for(int j = 1;j<=n;j++)
            if(dis[i][j]>dis[i][k]+disv[j][k])//顺序反正无所谓
                dis[i][j] = dis[i][v]+dis[j][v];

若在无权图中，判断连通性，可以直接改成

dis[i][j] = dis[i][j]||(dis[i][k]&&dis[k][j]);

Dijkstra

O($n^2$) 单源最短路径算法(计算起点只有一个的情况)，不能处理负边权的情况 描述 设起点为s，dis[v]表示s到v的最短路径，rep[v]为v的前驱节点，用于输出路径 A.初始化：dis[v] = $\infty$(v!=s);dis[s] = 0;pre[s] = 0; B.for(int i = 1;i<=n;i++){ 1.在没有访问过的点中找一个顶点u使得dis[u]是最小的 2.u标记为已确定的最短路径 3.for与u相连的每个未确定最短路径的顶点v

    if(dis[u]+w[u][v]<dis[v]){
        dis[v] = dis[u]+w[u][v];//dis[v] = min(dis[v],dis[u]+w[u][v]);
        pre[v] = u;
    }

} 个人认为迪斯特拉算法本质就是贪心+动规。每次都走最短的路径，在判断最短路径和之前的走法的最大最小距离，从而得到最优解。好暴力

链式前向星遍历

就是用数组模拟链表，提高效率 参考程序:

struct Edge{
    int next;//下一条边的编号
    int to;//这条边到达的点
    int dis;//这条边的长度
}edges[N];
int head[N],num_edge,n,m,u,v,d;
void add_edge(int from,int to,int dis){
    edge[++num_edge].next = head[from];//head数组储存的是上一个终点为from的节点
    edge[num_edge].to = to;
    edge[num_edge].dis = dis;
    head[from] = num_edge;//把当前节点的位置放进去方便下一个连接到此节点的节点访问
}

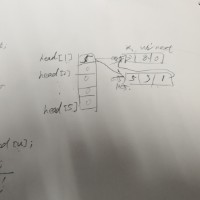
遍历从1开始的所有边：

for(int i = head[1];i!=0;i=edge[i].next){
    //do something
}

Ford福特算法

单源最短路径算法，可以处理负边权的情况，但不能处理存在负权回路的情况 时间复杂度O(NE)N是顶点数，E是边数 算法实现: 1.设s为起点，dis[s]即为s到v的最短距离，pre[v]为v的前驱，w[j]是边j的长度，且j连接u，v 2.初始化：dis[s] = 0,dis[v]=$\infty$(v!=s),pre[s]=0 看洛谷讲义

判断负权回路

for每条边(i,v)
    if(dis[u]+w<dis[v])return false;

若规定每条边都只走一次，就可以求出负权回路最短路径，bool数组mark一下嘛

SPFA算法

时间复杂度O(kE)k为常数，平均值2 思想： 初始时将起点入队，每次从队列中取出一个元素，并对所有与它相邻的点进行修改，若某个相邻的点修改成功，则将其入队，直到队列为空。

实现： 1dis[i]记录s到i的最路径,w[i][j]记录连接i、j的边的长度,pre[v]记录前驱

1. queue表示队列，head、tail指针 3.布尔数组exist[1…n]记录一个点是否在队列中 4.初始化dis[s] = 0;head = 0;tail = 1;exist[s]=true 5.

   do{
    1.头指针向下移，去除点u
    2.exit[u] = false;//即已经取出了队列
    3.for与u相连的所有点v//不要枚举所有点，数组模拟领接表储存
    if(dis[v]>dis[u]+w[u][v]){
        dis[v] = dis[u]+w[u][v];
        pre[v] = u;
        if(!exist[v]){//队列中不存在点v，v入队。因为v可以入队多次，与bfs相似而不同.其实可以直接改成true不管他，反正无所谓
        入队点v
        exist[v] = true;
           
        }
    }
   }while(head<tail);
   

   判断负环 若一个点进队的次数超过n次，则存在负环！

   输出最短路径(算法中用pre[x]记录)

   递归解决，pre[x]在之前的的数组

   void print(int x){
    if(pre[a][x]==0)return;
    print(pre[a][x]);
    cout<<"->"<<x;
   }
   

在主程序中先输出起点s，再，print(end);//因为它是倒着来的

图的连通性

其实就是改一下,判断距离改成bool判断连同就行