![luoguP4467 [SCOI2007]k短路](/images/posts/OI.png)
题面
题目描述
有$n$个城市和$m$条单向道路，城市编号为$1$到$n$。每条道路连接两个不同的城市，且任意两条道路要么起点不同要么终点不同，因此$n$和$m$满足$m \le n(n-1)$
给定两个城市a和b，可以给a到b的所有简单路（所有城市最多经过一次，包括起点和终点）排序：先按长度从小到大排序，长度相同时按照字典序从小到大排序。你的任务是求出a到b的第kk短路
输入输出格式
输入格式：
输入第一行包含五个正整数n, m, k, a, b。
以下m行每行三个整数u, v, l，表示从城市u到城市v有一条长度为l的单向道路。
输出格式：
如果a到b的简单路不足k条，输出No，否则输出第k短路：从城市a开始依次输出每个到达的城市，直到城市b，中间用减号”-“分割。
输入输出样例
输入样例# 1：
5 20 10 1 5
1 2 1
1 3 2
1 4 1
1 5 3
2 1 1
2 3 1
2 4 2
2 5 2
3 1 1
3 2 2
3 4 1
3 5 1
4 1 1
4 2 1
4 3 1
4 5 2
5 1 1
5 2 1
5 3 1
5 4 1
输出样例# 1：
1-2-4-3-5
输入样例# 2：
4 6 1 1 4
2 4 2
1 3 2
1 2 1
1 4 3
2 3 1
3 4 1
输出样例# 2：
1-2-3-4
输入样例# 3：
3 3 5 1 3
1 2 1
2 3 1
1 3 1
输出样例# 3：
No
解答
正解真的不会最短路径树太难了。所以骗分的方法是A*算法，可以卡到90分我不知道怎么回事，总要多MLE两个点，只卡到70分。
A*算法: 通过给不同状态不同的优先级，使对答案可能有贡献的状态排在前面，减少无用的搜索。 网上抄的两个图：
A*：
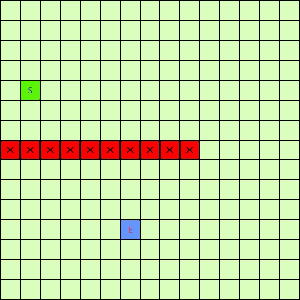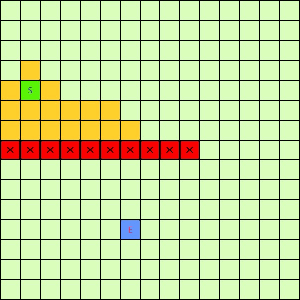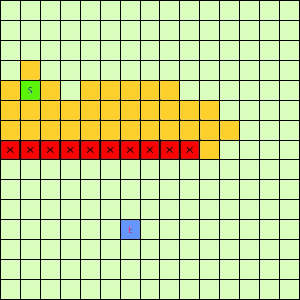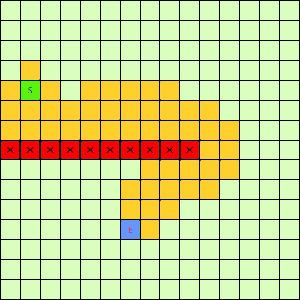BFS:
用$h(x)$表示走到当前点的权值和。$g(x)$表示估价函数。关于$h(x)$的计算很简单，就是一路走，一路加就行。但是$g(x)$怎么计算呢？建立反图后，我们可以事先跑一趟spfa它已经死了 dijkstra它太慢了 你喜欢的最短路径算法，计算出点$i$到点$b$的最短距离$dis[i]$，作为估价函数。然后把每个点放进小根堆里面，就是用堆代替BFS里面的队列，然后每次取出权值最小的点来跑，每次跑到点B以后就记录一下。如果到达k次，说明已经是第k短路了，那么直接输出。下图是感性理解
忽略灵魂画手
ATTENTION： 在结构体里面排序的时候，先按照权值大小排如果权值大小相同，就按路径字典序排，详情见代码。
# include <cstdio>
# include <cstring>
# include <queue>
# include <string>
using namespace std;
const int MAXN = 60;
const int MAXM = 2505;
int n,m,k;
int dis[MAXN];
bool vis[MAXN];
struct edge{int t,w,next;}edges1[MAXM],edges2[MAXM];
struct node{
int f,w;
int a[51];
int ptr = 0;
bool find(int x){
for(int i = 1;i<=ptr;i++){ if(x==a[i]){return true; }}
return false;
}
bool operator<(const node&n2)const{
if(w+dis[f]==n2.w+dis[n2.f]) {
int t = ptr>n2.ptr?n2.ptr:ptr;
for(int i = 1;i<=t;i++){
if(a[i]!=n2.a[i])return a[i]>n2.a[i];
}
return ptr>n2.ptr;
}
else return w+dis[f]>n2.w+dis[n2.f];
}
node& operator=(const node& n2){
f = n2.f;
w = n2.w;
for(int i = 1;i<=n2.ptr;i++){
a[i] = n2.a[i];
}
ptr = n2.ptr;
}
};
int head1[MAXN],head2[MAXN];
int top1,top2;
int read(){
int x = 0,f =1;
static char c =getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = x*10+c-'0';c = getchar();}
return x*f;
}
void add1(int f,int t,int w){//正图
edges1[++top1].next = head1[f];
edges1[top1].t = t;
edges1[top1].w = w;
head1[f] = top1;
}
void add2(int f,int t,int w){//反图
edges2[++top2].next = head2[f];
edges2[top2].t = t;
edges2[top2].w = w;
head2[f] = top2;
}
void spfa(){
memset(vis,false , sizeof(vis));
memset(dis,0x3f, sizeof(dis));
queue<int> q;
vis[n] = true;
dis[n] = 0;
q.push(n);
while(!q.empty()){
int f = q.front();
q.pop();
vis[f] = false;
for(int i = head2[f];i!=0;i = edges2[i].next){
int t = edges2[i].t;
if(dis[t]>dis[f]+edges2[i].w){
dis[t] = dis[f]+edges2[i].w;
if(!vis[t]){
vis[t] = true;
q.push(t);
}
}
}
}
}
bool found;
void Astar(int a,int b){
int cnt = 0;
priority_queue<node> q;
node no;no.f = a;no.w = 0;
no.a[++no.ptr] = a;
q.push(no);
while(!q.empty()){
node top = q.top();
q.pop();
if(top.f == b){
cnt++;
if(cnt>=k){
for(int i = 1;i<=top.ptr-1;i++){
printf("%d-",top.a[i]);
}
printf("%d",top.a[top.ptr]);
found = true;
return;
}
}
node temp;
for(int i = head1[top.f];i!=0;i = edges1[i].next){
int t = edges1[i].t;
if(!top.find(t)){
temp = top;
temp.f = t;
temp.w = top.w+edges1[i].w;
temp.a[++temp.ptr] = t;
q.push(temp);
}
}
}
}
int main(){
int a,b;
n = read(),m = read();
k = read();
a = read();
b = read();
int f,t,w;
for(int i = 1;i<=m;i++){
f = read(),t = read(),w = read();
add1(f,t,w);
add2(t,f,w);
}
spfa();
Astar(a,b);
if(!found)printf("No");
return 0;
}
