![luoguP1337 [JSOI2004]平衡点 / 吊打XXX](/images/posts/OI.png)
题面
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。 问绳结X最终平衡于何处。
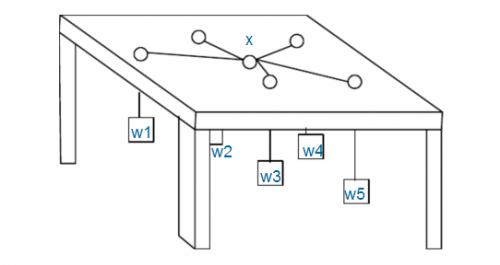
注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。
输入输出格式
输入格式：
文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。($-10000≤x,y≤10000, 0<w≤1000$ )
输出格式：
你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
输入输出样例
输入样例# 1：
3
0 0 1
0 2 1
1 1 1
输出样例# 1：
0.577 1.000
解答
正解：计算几何+正交分解(翘了那么久的课，怎么可能会嘛) AC算法传说中的模拟退火算法！ 关于模拟退火，可以参见百度百科
Simulate Annealing
首先，你要准备以下几个参数
初始温$度T$，降温系数$\Delta T$以及一个初始解(初始状态)
然后开始计算乱搞,计算流程如下
1.随机变化解，变化幅度为$T$ 2.计算新解与目前最优解的差为$\Delta E$ 2.判断当前解是否更优，即$\Delta$是否小于0，如果更优($Delta$小于0)，接受这个解 3.如果这个解不是更优的，以一定概率*接受它 4.降温
上文中提到的一定概率，经过无数科学家们的计算与分析实验，发现当此概率为\(e^{\frac{\Delta E}{kT }}\)时，最容易找到最优解，其中$\Delta E$是与当前最优解的差，$T$是当前温度，$k$是一个随机数。
为什么SA可能计算出最优解
以下仅为个人理解
我们把求解的过程比作在函数上找极点，如图
如果我们当前在一个解，然后我们通过随机数，获得一个变化幅度，获得一个新解，如果这个解更优，那当然是选择它呀！但是如果这个解不是更优呢？对于贪心算法，那就是选择放弃它。但是从图中可以看出，当前局部最优解可能不是全局最优解，为了找到全局最优解，我们还是得以一定概率接受它。但是如果它就是全局最优解呢？岂不是就走出去了吗？别担心！我们还会走回来的，并且随着温度的降低，接受一个更劣解的概率会越来越小！
借用洛谷日报的几张图方便理解：
但是也有它不适应的情况：解的变化随着解空间变大得太厉害了：
所以模拟退火仅限于函数峰不是特别多的情况(单调函数和单峰函数用二分三分啊，为什么要用SA?)
对于函数峰特别多的情况，分块跑SA再合并
一些小技巧
尽量多跑SA，但是又不能超时，那我就卡着时间来：
long s = clock(0);
while(double(clock()-s)/CLOCKS_PER_SEC<=0.7)//注意这里不用太贪心，把时间卡太死了，不然一下就是全部TLE。。。
simulate_annealing();
调参方法： 调小降温系数，调大初始温度，调大初始解。但是修改会导致运行时间变长。最好还是卡时间！ 以下是洛谷上AC代码：
# include <iostream>
# include <cstdlib>
# include <cmath>
# include <time.h>
# include <cstdio>
using namespace std;
inline int read(){
char ch = getchar();
int f = 1 ,x = 0;
while(ch > '9' || ch < '0'){if(ch == '-')f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + ch - '0';ch = getchar();}
return x * f;
}
struct node{
double x,y;
int wei;
}nodes[1010];
int n;
long s ;
double abbs(double a){return a<0?-a:a;}
double cal(double x,double y){
double ans = 0.0;
for(int i = 1;i<=n;i++){
double dis = (x-nodes[i].x)*(x-nodes[i].x)+(y-nodes[i].y)*(y-nodes[i].y);
dis = sqrt(dis);
ans+=dis*nodes[i].wei;
}
return ans;
}
double T ;
const double delta = 0.99789999;
double ans_x,ans_y,ans = 1e15+7;
double nx,ny;
const double ep = 1e-14;
void simulated_annealing(){
T = 1926;
while(T>ep) {
nx = ans_x+(rand() * 2 - RAND_MAX) * T;
ny = ans_y+(rand()*2-RAND_MAX)*T;
double new_ans = cal(nx,ny);
double DE = new_ans-ans;
if(DE<0){
ans = new_ans;
ans_x = nx;
ans_y = ny;
}else if(exp(-DE/T)*RAND_MAX>rand()){
ans = new_ans;
ans_x = nx;
ans_y = ny;
}
T*=delta;
}
}
void SA(){
while(double(clock()-s)/CLOCKS_PER_SEC<=0.7)
simulated_annealing();
}
int main() {
n = read();
s = clock();
for(int i = 1;i<=n;i++){
nodes[i].x = read();
nodes[i].y = read();
nodes[i].wei = read();
}
SA();
printf("%.3lf %.3lf",ans_x,ans_y);
return 0;
}
