网络流
概念
若有向图G=(V,E)满足下列条件
- 有且仅有一个顶点S,它的入度为零,即d-(S) ==0,这个顶点S便称为源点,或称为发点。
- 有且仅有一个顶点T,它的出度为零,即d+(T) = 0,这个顶点T便称为汇点,或称为收点
- 每一条弧都有非负数,叫做该边的容量。边(vi, vj)的容量用$C_{i,j}$表示
则称之为网络流图,记为G = (V, E, C)
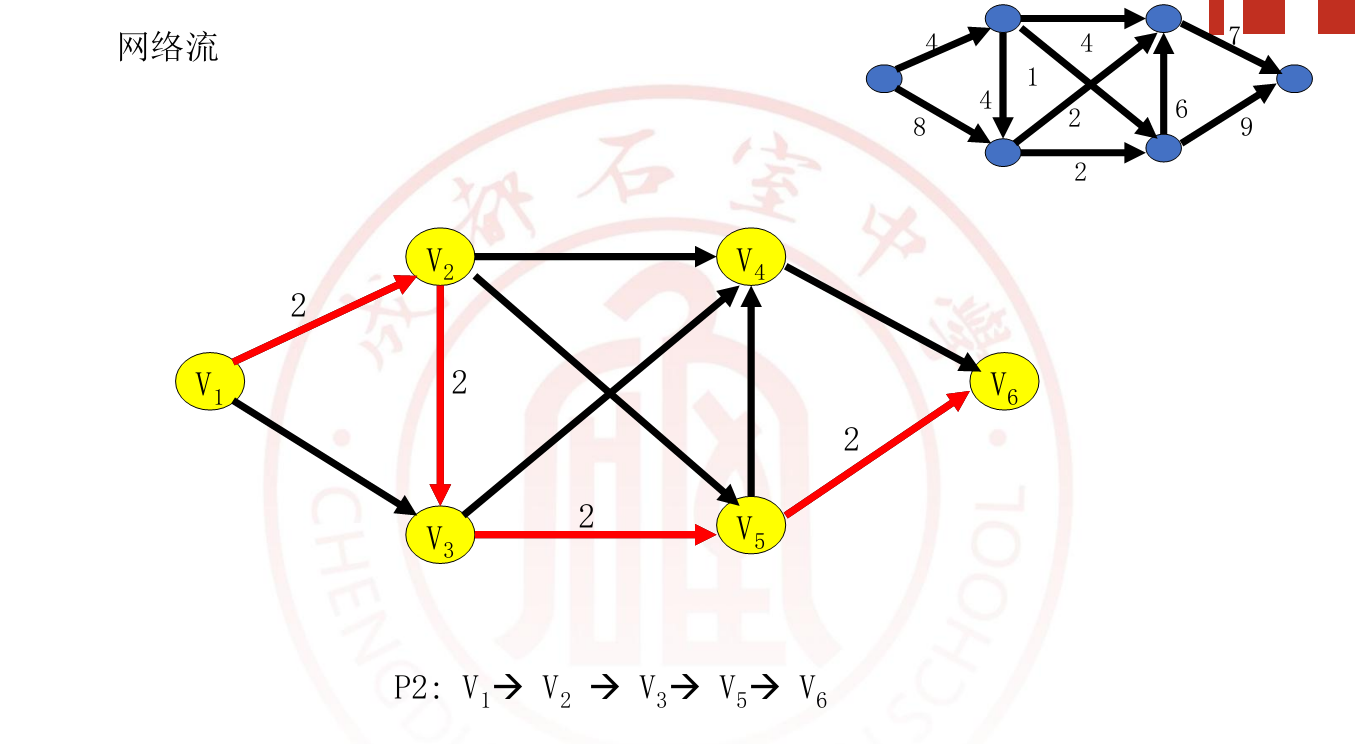
可行流
其实就是每一条弧上面的流量$F_{i,j}$都小于这条路的容量。性质如下
- $F_{i,j}\leq C_{i,j}$
- 除源点和汇点以外,其他点均有$F_{i,j} = \sum F_{j,k}$
- 反对称性:即$F_{i,j} = -F_{j,i}$
还有一些概念
饱和弧:网络中Fij =Cij的弧 非饱和弧:网络中Fij < Cij的弧 非零流弧:网络中 Fij>0 的弧 零流弧:网络中 Fij =0的弧
前向弧和后向弧之类的东西就看看讲义好了
在图G中,一个由不同的边组成的序列e1,e2,…,eg,如果ei是连接Vi-1与Vi(i=1,2,…,g)的,我们就称这个序列为从V0到Vg的一条道路,数g称为路长,V0与Vg称为这条道路的两个端点,Vi(1<=i<=g-1)叫做道路的内点。
残量网络
其实就是跑过一次网络流以后剩下的容量,方便计算
- 为了更方便算法的实现,一般根据原网络定义一个残量网络。其中r(u,v)为残量网络的容量
- r(u,v) = c(u,v) – f(u,v)
- 通俗地讲:就是对于某一条边(也称弧),还能再有多少流量经过
- Gf残量网络,Ef表示残量网络的边集
建立后向弧
后向弧为算法纠正自己所犯的错误提供了可能性,它允许算法取消先前的错误的行为。
图示

图二中,有些方向相反的边就是后向弧
注意,后向弧只是概念上的,在程序中后向弧与前向弧并无区别.我们为所有边设置反向边(容量为0),并将其流量与正向边同步。为了保持T->S边流量为0,每当由于增广操作,T->S边流量上升,其反向边也同步上涨,而显然在残量网络中反向边是沿S->T方向的,这就又出现了一条增广路,计算机对此无法容忍,下调它的流量,我们的T->S边流量也随之回到了0,达到了目的
割
G = (V, E, C)是已知的网络流图,设U是V的一个子集,W =V\U,满足S ∈ U,T∈W。即U、W把V分成两个不相交的集合,且源点和汇点分属不同的集合(其实就是把一个网络流图分成2部分,源点和汇点分别属于不同集合就完了)对于弧尾在U,弧头在W的弧所构成的集合称之为割切,用(U,W)表示。把割切(U,W)中所有弧的容量之和叫做此割切的容量,记为C(U,W),即: \(C(U,V) = \sum_{i\in U\ \ j\in V}C_{i,j}\)
图中令$U = {S, V1}$,则$W = {V2, V3, V4, T}$,那么,$C(U, W) = <S, V2> + <V1, V2> + <V1, V3>+<V1, V4>=8+4+4+1=17$
要理解割,网上找的图装逼之二 最小割与最大流(mincut & maxflow)



增广路算法求最大流
几个定理
- 对于已知的网络流图,设任意一可行流为f,任意一割切为(U, W),必有:$V(f) \leq C(U, W)$
- 可行流f是最大流的充分必要条件是:f中不存在增广路
- 整流定理:如果网络中所有的弧的容量是整数,则存在整数值的最大流
- 最大流最小割定理:最大流等于最小割,即max V(f) = min C(U, W)。(其实就是限制边的集合)
EK算法(了解一下就好了)
第1步,令$x=(xij)$是任意整数可行流,可能是零流,给s一个永久标号$(-, ∞)$。 • 第2步(找增广路),如果所有标号都已经被检查,转到第4步。 找到一个标号但未检查的点i, 并做如下检查, • 对每一个弧(i,j),如果$xij<Cij$, 且j未标号,则给j一个标号$(+i, δ (j) )$, 其中, $δ (j)=min{Cij-xij , δ (i) }$ • 对每一个弧(j, i),如果xji>0,且j未标号,则给j一个标号$(-i, δ (j) )$, 其中,$ δ (j)=min(xji , δ (i) )$ • 第三步(增广),由点t开始,使用指示标号构造一个增广路,指示标号的正负 则表示通过增加还是减少弧流量来增加还是减少弧流量来增大流量,抹去s点 以外的所有标号,转第二步继续找增广轨。 • 第四步(构造最小割),这时现行流是最大的,若把所有标号的集合记为S,所 有未标号点的集合记为T,便得到最小容量割(S,T)。
Dinic算法——按层次计算最大流
基本思想:使用BFS建立层次,并通过阻塞流来增广 层次图:假设在残留网络中,起点到结点u的距离是dist[u],就把dist[u]看做是点u的“层次”。保留每个点出发到下个层次的弧,即只保留dist[u]+1=dist[v]的边(u,v),得到的图就是层次图。层次图上任意路径都是:起点->层次1->层次2->…->T 的顺序,而且每条这样的路都是S-T的最短路。(其实就是BFS的深度)
阻塞流
就是指不考虑反向弧时的极大流。对应到程序就是从起点开始在层次图上DFS,每找到一条就增广。

 eg板子题:水谷3376
eg板子题:水谷3376
# include <cstdio>
# include <algorithm>
# include <iostream>
# include <queue>
# include <cstring>
using namespace std;
const int MAXN = 4010000;
const int INF = 0x3f3f3f3f;
struct edge{int t,f,w,next,c;bool operator<(const edge &e2)const {return w>e2.w; }} edges[MAXN<<2];//c是容量 f是流量
int head[MAXN],top = 1;
int map[43][43];
int n ,m;
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
void add(int f,int t,int w) {
edges[++top].next = head[f];
edges[top].t = t;
edges[top].c = w;
head[f] = top;
}
int S,T;
int dep[MAXN];
bool bfs(){//判断是否还能到达汇点的同时分层
memset(dep,-1,sizeof(dep));
queue<int> q;
q.push(S);
dep[S] = 0;
bool flag = false;
while(!q.empty()){
int top = q.front();q.pop();
for(int i = head[top];i;i = edges[i].next){
int t = edges[i].t;
if(dep[t]!=-1||edges[i].c<=0)continue;
dep[t] = dep[top]+1;
q.push(t);
if(t==T)flag = true;//到达了汇点
}
}
return flag;
}
int cur[MAXN];//当前点优化,在一开始的时候和head一样。后面细说
int dfs(int x,int f){//f是最小惨量
if(x==T||f==0)return f;//到了汇点或者流量已用完
int used = 0;//当前点已经流出的流量
for(int &i = cur[x];i;i = edges[i].next){//这个优化就是防止重复的走到同一个点的情况,因为这一个点已经走过了,没必要在拓展,就把这条边直接不考虑了
int t = edges[i].t;
if(edges[i].c>0&&dep[x]==dep[t]-1){
int w = dfs(t,min(f,edges[i].c));
if(!w)continue;//走不动了
used+=w;f-=w;
edges[i].c-=w;edges[i^1].c+=w;//正反边更新
if(f==0)break;//流量已经用完了,就不更新了
}
}
if(!used)dep[x] = -1;//这个点走不动了
return used;
}
int dinic(){
int maxFlow = 0;
while (bfs()){
for(int i = 1;i<=n;i++)cur[i] = head[i];
maxFlow+=dfs(S,INF);
}
return maxFlow;
}
int main(){
n = read();m = read();S = read(),T = read();
for(int i = 1;i<=m;i++){
int f = read(),t = read(),c = read();
add(f,t,c);
add(t,f,0);
}
printf("%d",dinic());
return 0;
}
所以Dinic复杂度$O(N^2M)$
- 最多有n个阶段,即最多构建n个层次,每个层次用bfs一遍即可得到,1次bfs是M,所有构建层次图总时间O(NM)
- 一次dfs是O(nm),最多n次dfs,所以找可增广需O(NNM)也是整个算法的复杂度
二分图的网络流模型建模
eg「网络流 24 题」搭配飞行员
把所有正飞行员全部连接到0号点上,容量为1,副飞行员连到n+1号点上,容量为1,求个最大流就行了。

# include <cstdio>
# include <cstring>
# include <queue>
using namespace std;
const int MAXN = 110;
const int MAXM = 710;
struct edge{int c,t,next;}edges[MAXM];
int top = 1;
int n,m;
const int INF = 0x3f3f3f;
int head[MAXN];
void add(int f,int t,int c){
edges[++top].next = head[f];
edges[top].t = t;
edges[top].c = c;
head[f] = top;
}
int dep[MAXN];
int S,T;
int curr[MAXN];
bool bfs(){//判断是否还能到达汇点的同时分层
memset(dep,-1,sizeof(dep));
queue<int> q;
q.push(S);
dep[S] = 0;
bool flag = false;
while(!q.empty()){
int top = q.front();q.pop();
for(int i = head[top];i;i = edges[i].next){
int t = edges[i].t;
if(dep[t]!=-1||edges[i].c<=0)continue;
dep[t] = dep[top]+1;
q.push(t);
if(t==T)return true;//到达了汇点
}
}
return false;
}
int cur[MAXN];//当前点优化,在一开始的时候和head一样。后面细说
int dfs(int x,int f){//f是最小惨量
if(x==T||f==0)return f;//到了汇点或者流量已用完
int used = 0;//当前点已经流出的流量
for(int &i = cur[x];i;i = edges[i].next){//这个优化就是防止重复的走到同一个点的情况,因为这一个点已经走过了,没必要在拓展,就把这条边直接不考虑了
int t = edges[i].t;
if(edges[i].c>0&&dep[x]==dep[t]-1){
int w = dfs(t,min(f,edges[i].c));
if(!w)continue;//走不动了
used+=w;f-=w;
edges[i].c-=w;edges[i^1].c+=w;//正反边更新
if(f==0)break;//流量已经用完了,就不更新了
}
}
if(!used)dep[x] = -1;//这个点走不动了
return used;
}
int dinic(){
int maxFlow = 0;
while (bfs()){
for(int i = 1;i<=S;i++)cur[i] = head[i];
maxFlow+=dfs(S,INF);
}
return maxFlow;
}
int main(){
scanf("%d%d",&n,&m);
int f,t;
S = n+2,T = n+1;
while(scanf("%d%d",&f,&t)!=EOF){
add(f,t,1);
add(t,f,0);
}
for(int i = 1;i<=m;i++)add(S,i,1),add(i,S,0);
for(int i = m+1;i<=n;i++)add(i,T,1),add(T,i,0);
printf("%d",dinic());
return 0;
}
三分匹配等等
如 [USACO07OPEN]吃饭Dining其实就是把奶牛,食物,水连在源点S,奶牛拆成2个点,中间用容量为1的边连接起来,再连接饮料,然后连接汇点T。跑最大流
最大流量最小费用
其实就是把bfs改成spfa或者dijkstra,因为这样走的就是费用最小的一条路,然后跑dinic; luogu3381
# include <iostream>
# include <cstring>
# include <queue>
using namespace std;
const int MAXN = 5010;
const int MAXM = 50010;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const int intINF = 0x3f3f3f3f;
struct edge{int t,next;long long cap,w;}edges[MAXM<<1];
int top = 1,head[MAXN];
void add(int f,int t,int cap,int w){
edges[++top].next = head[f];
edges[top].t = t;
edges[top].cap = cap;
edges[top].w = w;
head[f] = top;
}
bool vis[MAXN];
long long dis[MAXN];
int S,T,n,m;
bool spfa(){
memset(vis,false,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
vis[S] = true;
queue<int> q;
q.push(S);
dis[S] = 0;
while(!q.empty()){
int top = q.front();q.pop();
vis[top] = false;
for(int i = head[top];i;i = edges[i].next){
int t = edges[i].t;
if(dis[t]>dis[top]+edges[i].w&&edges[i].cap>0){
dis[t] = dis[top]+edges[i].w;
if(!vis[t]){
vis[t] = true;
q.push(t);
}
}
}
}
return dis[T]!=INF;
}
int curr[MAXN];
long long dfs(int x,long long flow){
vis[x] = true;
if(x==T||flow==0)return flow;
long long used = 0;
for(int &i = curr[x];i;i = edges[i].next){
int t = edges[i].t;
if(!vis[t]&&dis[t]==dis[x]+edges[i].w&&edges[i].cap>0){
int w = dfs(t,min(flow,edges[i].cap));
if(w==0)continue;
flow-=w;used+=w;
edges[i].cap-=w;edges[i^1].cap+=w;
if(flow==used)return used;
}
}
return used;
}
long long maxflow,mincost,mindis;
void dinic(){
while(spfa()){
for(int i = 0;i<=n;i++)curr[i] = head[i];
memset(vis,false,sizeof(vis));
int w = dfs(S,INF);
maxflow+=w;
mincost+=w*dis[T];
}
}
int main(){
int f,t;
ios::sync_with_stdio(false);
long long ci,wi;
cin>>n>>m;cin>>S>>T;
for(int i = 1;i<=m;i++){
cin>>f>>t>>ci>>wi;
if(ci==0)continue;
add(f,t,ci,wi);
add(t,f,0,-wi);
}
dinic();
cout<<maxflow<<' '<<mincost;
return 0;
}
