T1
给定一颗N个节点的树,定义两点距离为他们之间路径中边权最小值。
Q次询问K,V,询问到V距离>=K的点有多少(不含V)
输入
第一行两个整数N,Q。
接下来N-1行,每行3个整数u,v,w表示u,v之间有条路径,长为w
接下来Q组询问,每组询问2个整数k,V
输出
Q行回答询问
样例输入
4 3
1 2 3
2 3 2
2 4 4
1 2
4 1
3 1
样例输出
3
0
2
提示 对于30%的数据,1≤N,Q≤1000。
对于70%的数据,1≤N≤2000,Q≤10^5。
对于100%的数据,1≤N,Q≤10^5, 1≤w,K≤10^9.
解答
我们考虑并查集维护。把所有询问离线下来,把询问的值从大到小排序,然后再把每一条边也从大到小排序。处理每个询问的时候,把每一条边从大到小加入并查集,知道边权小于查询的边权。这样并查集中的点数,就是答案。注意并查集在合并的时候,合并权重不可以这样写void unionn(int x,int y){fa[find(y)]=find(x);wei[find(x)]+=wei[find(y)];},因为前面y经过路径压缩已经把父节点改为fa[x]了,所以后面更新权重的时候就不能那样做。 代码:
# include <cstdio>
# include <cstring>
# include <algorithm>
using namespace std;
const int MAXN = 100010;
const int MAXM = MAXN-1;
const int INF = 0x3f3f3f3f;
struct edge{int f,t,w,next;bool operator<(const edge &e2)const {return w>e2.w; }} edges[MAXM<<1];
int n ,Q;
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
struct query{int len,root,id,ans;}querys[(int)1e5+10];
int fa[MAXN];
int wei[MAXN];
int find(int x){
return fa[x]==x?x:fa[x] = find(fa[x]);
}
void unionn(int x,int y){
int fx = find(x);int fy = find(y);
fa[fy] = fx;
wei[fx]+=wei[fy];
}
bool cmp1(const query&q1,const query&q2){
return q1.len>q2.len;
}
bool cmp2(const query&q1, const query &q2){
return q1.id<q2.id;
}
int main(){
n = read();Q = read();
int f,t,w;
for(int i = 1;i<=n-1;i++){
f = read(), t = read(),w = read();
edges[i].f = f;edges[i].t = t; edges[i].w = w;
}
int root,K;
for(int i = 1;i<=Q;i++){
K = read(),root = read();
querys[i].len = K;querys[i].root = root;
querys[i].id = i;
}
sort(querys+1,querys+Q+1,cmp1);
sort(edges+1,edges+n);
int pos = 1;
for(int i = 1;i<=n;i++)fa[i] = i,wei[i] = 1;
for(int i = 1;i<=Q;i++){
while(pos<n&&edges[pos].w>=querys[i].len)unionn(edges[pos].f,edges[pos].t),pos++;
querys[i].ans = wei[find(querys[i].root)]-1;
}
sort(querys+1,querys+Q+1,cmp2);
for(int i = 1;i<=Q;i++){
printf("%d\n",querys[i].ans);
}
return 0;
}
T2
题面
给定一个迷宫,构成一棵有根树,你开始在根节点,出口是每个叶子节点,L可以在每个出口放一个守卫,每1个单位时间内,你和守卫都可以移动到相邻的一个点,如果某一时刻 守卫与你相遇了(在边上或点上均算),则你将被抓住。问为了保证抓住你,L最少需要几个守卫。
输入
第1行包含2个用空格分开的正整数n、K,表示有n个节点,K表示根节点编号
接下来n-1行,每行2个整数u,v,表示u到v有条路径
输出
输出1个整数。
样例输入
7 1
1 2
1 3
3 4
3 5
4 6
5 7
样例输出
3
提示 N<=100000
解答
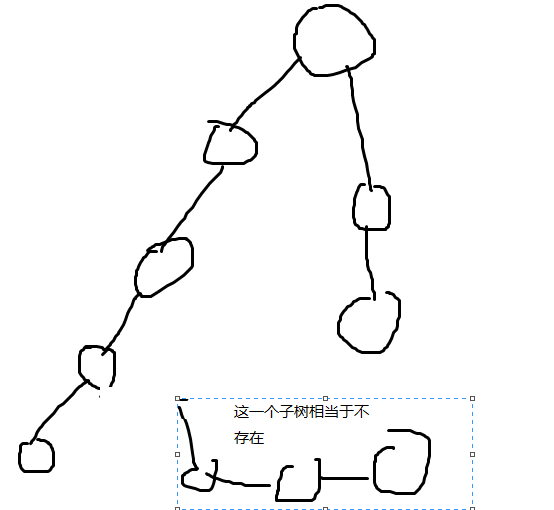
其实考试的时候算是想到半个正解了的吧。求出根节点到每个节点的深度dep[x],再求出叶节点到每个节点的深度dep2x,因为要拦截,所以对于每个点必须要$dep2[x]>dep[x]$。你可看下图,去了最小之后,就相当于把一些分枝砍掉了。然后对于一个节点要防到,所以在假设对方不存在的情况下,必须保卫者先走到才行。所以从上到下搜对于dep2[x]<=dep[x]的点,需要一个保卫,就ans++就行了
# include <cstdio>
# include <cstring>
const int MAXN = 100010;
const int MAXM = MAXN-1;
const int INF = 0x3f3f3f3f;
struct edge{int t,w,next;bool operator<(const edge &e2)const {return w>e2.w; }} edges[MAXM<<1];
int head[MAXN],top = 1;
int n ,K;
int read(){
int x = 0,f = 1;
static char c = getchar();
while(c<'0'||c>'9'){ if(c=='-')f = -1;c = getchar(); }
while(c>='0'&&c<='9'){ x = (x<<1)+(x<<3)+c-'0';c = getchar(); }
return x*f;
}
void add(int f,int t,int w) {
edges[++top].next = head[f];
edges[top].t = t;
edges[top].w = w;
head[f] = top;
}
int dep1[MAXN],dep2[MAXN];
bool vis[MAXN];
inline int min(int a,int b){return a<b?a:b;}
void dfs(int x,int fa){
vis[x] = true;
dep1[x] = dep1[fa]+1;
dep2[x] = INF;
for(int i = head[x];i;i = edges[i].next){
int t = edges[i].t;
if(vis[t])continue;
dfs(t,x);
dep2[x] = min(dep2[t]+1,dep2[x]);
}
if(dep2[x]==INF)dep2[x] = 1;
}
int ans;
bool vis2[MAXN];
void work(int x){
vis2[x] = true;
if(dep2[x]<=dep1[x]){
ans++;
return;
}
for(int i = head[x];i;i = edges[i].next){
int t = edges[i].t;
if(vis2[t])continue;
work(t);
}
}
int main(){
n = read();K = read();
int f,t;
for(register int i = 1;i<=n-1;i++){
f = read(),t = read();
add(f,t,1);
add(t,f,1);
}
dfs(K,0);
work(K);
printf("%d",ans);
return 0;
}
