题面
描述
国际象棋中骑士的移动规则和中国象棋中的马是类似的，它先沿着一个方向移动两格，再沿着与刚才移动方向垂直的方向移动一格。路径上的棋子并不会影响骑士的移动，但是如果一个骑士走到了一个放有棋子的格子，它就会攻击那棋子。 现在有一个 n∗n的棋盘，有k个骑士需要被摆到棋盘上去。那么使所有骑士互不攻击的摆放方式一共有多少种呢？
输入
一行: 两个整数， n,k
输出
一行: 一个整数，为摆放的方式数
样例输入
样例[1]
3 2
样例[2]
4 4
样例输出
样例[1]
28
样例[2]
412
提示 数据范围及提示 Data Size & Hint $1≤n≤8,1≤k≤n^2$
解答
我们可以发现，最多的k不超过$\frac{n}{2}$个。然后画图分析
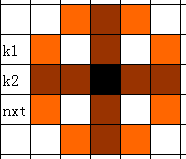图中黄色表示可以被攻击到的地方。我们发现每个状态会被上一行的状态影响，同时影响下一行的状态。我们用dp[i][j][k1][k2]表示i行，当前用了j个骑士，上一行的状态为k1，当前行的状态为k2的情况的方案数，然后通过枚举状态进行转移。复杂度$O(n\times m\times 2^{2n})$
我们还可以小小地优化一下，预处理出合法的状态。L1[i][j]表示状态i和状态j挨着的时候是否合法，L2表示i和j隔一行的时候是否合法。
写一个check函数:
bool check(int x,int y,int d){
if((x&(y<<d))||(x&(y>>d)))return false;
return true;
}
代码：
# include <iostream>
using namespace std;
int dp[9][33][256][256];
int w,h;
bool L1[256][256];
bool L2[256][256];
inline int lowbit(int x){return x&-x;}
int n,k,states;
int cnt[256];
bool check(int x,int y,int d){
if((x&(y<<d))||(x&(y>>d)))return false;
return true;
}
int getBit(int x){
int ans = 0;
while(x)ans++,x-=lowbit(x);
return ans;
}
int main(void){
cin>>n>>k;states=1<<n;
for(int i = 0;i<states;i++){
cnt[i] = getBit(i);
for(int j = 0;j<states;j++){
L1[i][j] = L1[j][i] = check(i,j,2);//前一行的状态，因为左右各走2格，然后向上下走一格，所以偏移量是2
L2[i][j] = L2[i][j] = check(i,j,1);//同理,上下走2格，向下走一格，偏移量为1
}
}
dp[0][0][0][0] = 1;
for(int i = 0;i<n;i++){
for(int j = 0;j<=k;j++){
for(int k1 = 0;k1<states;k1++){//上一行
for(int k2 = 0;k2<states;k2++){//当前行
if(dp[i][j][k1][k2]){//有值表示当前行和上一行合法
for(int nxt = 0;nxt<states;nxt++){
if(L2[k1][nxt]&&L1[nxt][k2]&&j+cnt[nxt]<=k){//当前行和下一行合法，上一行和当前行的下一行合法，并且骑士数量小于k个
dp[i+1][j+cnt[nxt]][k2][nxt]+=dp[i][j][k1][k2];
}
}
}
}
}
}
}
long long ans = 0;
for(int i = 0;i<states;i++){
for(int j = 0;j<states;j++){
ans+=dp[n][k][i][j];
}
}
cout<<ans;
return 0;
}
