题面
举行计算机科学家盛宴的大厅的地板为 M∗N(1≤M≤9,1≤N≤9)的矩形。现在必须要铺上硬木地板砖。可以使用的地板砖形状有两种： 1)2∗1 的矩形砖 2)2∗2 中去掉一个 1∗1 的角形砖 你需要计算用这些砖铺满地板共有多少种不同的方案。 注意：必须盖满，地板砖数量足够多，不能存在同时被多个板砖覆盖的部分。
输入
一行，两个整数： M,N
输出
输出方案总数，如果不可能那么输出 0 。
样例输入
2 3
样例输出
5
解答
状态压缩DP。每块砖会影响2行。如图
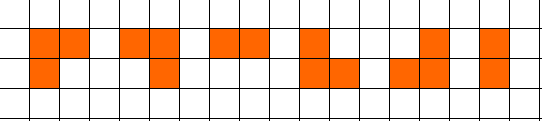然后就是dfs转移状态就好了。见注释：
# include <iostream>
using namespace std;
long long dp[11][1000];
int w,h,states;
# define add(a,k) (a|(1<<k))
# define exist(a,k) (!(a&(1<<k)))
void dfs(int line,int s1,int s2,int d){//s1当前行，s2下一行
if(d==w){
dp[line+1][s2]+=dp[line][s1];
return;
}
if(exist(s1,d)){
if(exist(s2,d)){
dfs(line,s1,add(s2,d),d+1);//竖着2个的
if(d+1<w&&exist(s2,d+1))dfs(line,s1,add(add(s2,d),d+1),d+1);//缺角的
if(d>0&&exist(s2,d-1))dfs(line,s1,add(add(s2,d),d-1),d+1);//缺角的
}
if(d<w-1&&exist(s1,d+1)){
dfs(line,s1,s2,d+2);//横着的
if(exist(s2,d))dfs(line,s1,add(s2,d),d+2);//缺角的
if(exist(s2,d+1))dfs(line,s1,add(s2,d+1),d+2);//缺角的
}
}else{
dfs(line,s1,s2,d+1);
}
return;
}
int main(){
cin>>h>>w;
states = 1<<w;
dp[1][0]= 1;
dfs(1,0,0,0);
for(int i = 2;i<=h;i++){
for(int j = 0;j<states;j++){
dfs(i,j,0,0);
}
}
if(w*h==1){
cout<<0<<endl;
return 0;
}
cout<<dp[h+1][0];
return 0;
}
