高斯消元
就是求解线性方程组。写成矩阵的形式,最后把它换成三角矩阵。
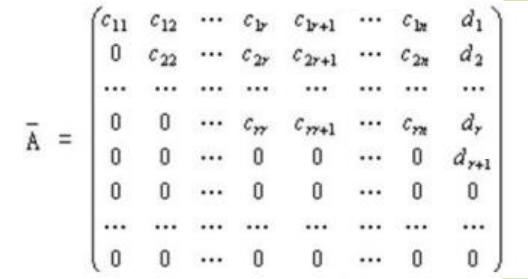
然后再向上带入就好了 eg1: 贾老二算算术 描述 贾老二是个品学兼优的好学生,但由于智商问题,算术学得不是很好,尤其是在解方程这个方面。虽然他解决 2x=2 这样的方程游刃有余,但是对于 {x+y=3 x-y=1} 这样的方程组就束手无策了。于是他要你来帮忙。前提是一次方程组且保证在integer的范围内可以处理所有问题。 输入 第一行一个数字N(1≤N≤100)表示要求的未知数的个数,同时也是所给的方程个数。 第2到N+1行,每行N+1个数。前N个表示第1到N个未知数的系数。第N+1个数表示N个未知数乘以各自系数后的加和。(保证有唯一整数解) 输出 一行N个数,表示第1到N个未知数的值(四舍五入保留整数)。 样例输入
2
1 1 3
1 -1 1
样例输出
2 1
代码:
# include <iostream>
# include <cmath>
using namespace std;
double a[110][110],ans[110];
int n;
void deal(int k){//化简,注意每一行只会影响以下的行。
double p;int x = k;
for(int i = k+1;i<=n;i++){
if(abs(a[i][k])>abs(a[x][k]))x = i;//为了减少误差,把每个未知数系数最大的作为主元
}
if(x!=k)for(int j = k;j<=n+1;j++)swap(a[x][j],a[k][j]);//交换行
for(int i = k+1;i<=n;i++){
p = a[i][k]/a[k][k];
for(int j = k;j<=n+1;j++)a[i][j] -= p*a[k][j];//消元
}
}
void guass(){
for(int i = 1;i<=n;i++)deal(i);
for(int i = n;i>0;i--){//自底向上求解
for(int j = n;j>i;j--){
a[i][n+1]-=a[i][j]*ans[j];
}
ans[i] = a[i][n+1]/a[i][i];
}
}
int main(){
cin>>n;
for(int i = 1;i<=n;i++)for(int j = 1;j<=n+1;j++)cin>>a[i][j];
guass();
for(int i = 1;i<=n;i++)cout<<(int)(ans[i]+0.5)<<' ';
return 0;
}
