题面
输入n个矩形,求他们总共占地面积(也就是求一下面积的并)
输入
可能有多组数据,读到n=0为止(不超过500组) 每组数据第一行一个数n,表示矩形个数(n<=100) 接下来n行每行4个实数x1,y1,x2,y1(0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000),表示矩形的左下角坐标和右上角坐标. 他们的边是平行于x坐标轴,和y坐标轴。
输出
一行表示答案,保留2位小数
样例输入
2
10 10 20 20
15 15 25 25.5
样例输出
180.00
解答
用线段树维护当前扫描到的矩形的下底,如图所示(图片来自hzwer)
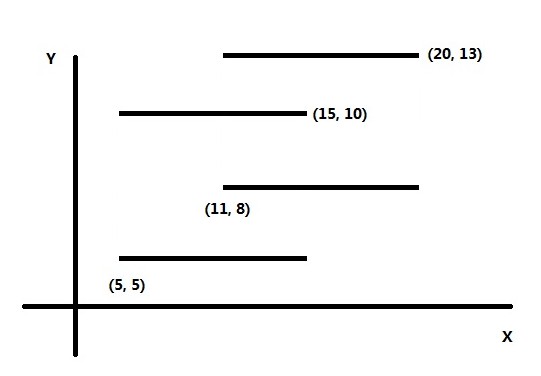
然后从下到上计算面积。其他的我今天不想写 参考博客
# include <iostream>
# include <cstring>
# include <cstdio>
# include <algorithm>
# define clear(x) memset(x,0,sizeof(x))
using namespace std;
const int MAXN = 210;
struct line{
double x1,x2,y;
int flag;
bool operator<(const line &l2)const{return y<l2.y;}
}lines[MAXN];
double HASH[MAXN],sum[MAXN<<2];
int col[MAXN<<2];
void pushup(int size,int l,int r){
if(col[size])sum[size] = HASH[r+1]-HASH[l];
else if(l==r)sum[size] = 0;
else sum[size] = sum[size<<1]+sum[size<<1|1];
}
void update(int L,int R,int flag,int l,int r,int size){
if(L<=l&&R>=r){
col[size]+=flag;
pushup(size,l,r);
return;
}
int mid = l+r>>1;
if(L<=mid)update(L,R,flag,l,mid,size<<1);
if(R>mid)update(L,R,flag,mid+1,r,size<<1|1);
pushup(size,l,r);
}
int main(){
int n;
while(cin>>n){
if(n==0)break;
double x1,x2,y1,y2;
for(int i = 1;i<=n;i++){
cin>>x1>>y1>>x2>>y2;
lines[i*2-1].x1 = lines[i*2].x1 = x1;
lines[i*2-1].x2 = lines[i*2].x2 = x2;
lines[i*2-1].y = y1;lines[i*2].y = y2;
lines[i*2-1].flag = 1;lines[i*2].flag = -1;
HASH[2*i-1] = x1;HASH[2*i] = x2;
}
sort(lines+1,lines+2*n+1);
sort(HASH+1,HASH+2*n+1);
clear(col),clear(sum);
double ans = 0;
for(int i = 1;i<=2*n;i++){
int l = lower_bound(HASH+1,HASH+2*n+1,lines[i].x1)-HASH;
int r = lower_bound(HASH+1,HASH+2*n+1,lines[i].x2)-HASH-1;//处理两条直线重复的地方
if(l<=r)update(l,r,lines[i].flag,1,2*n,1);
ans+=sum[1]*(lines[i+1].y-lines[i].y);
}
printf("%.2f\n",ans);
}
}
