![woj3604 [POI2014]HOT_Hotels(数据有加强）](/images/posts/OI.png)
题面
有一个树形结构的宾馆，n (1≤n≤100 000)个房间，n-1条无向边，每条边的长度相同，任意两个房间可以相互到达。吉丽要给他的三个妹子各开（一个）房（间）。三个妹子住的房间要互不相同（否则要打起来了），为了让吉丽满意，你需要让三个房间两两距离相同。 有多少种方案能让吉丽满意？
输入
第一行一个数n。 接下来n-1行，每行两个数x,y，表示x和y之间有一条边相连。
输出
让吉丽满意的方案数。
样例输入
7
1 2
5 7
2 5
2 3
5 6
4 5
样例输出
5
解答
神仙状态。
画画图可以发现有如下两种可能：
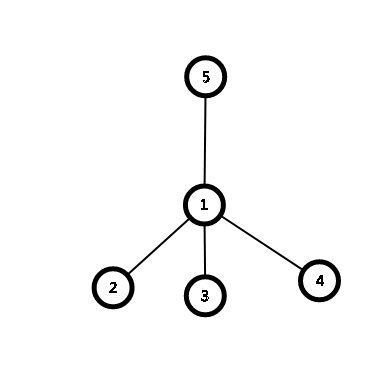(此时5是根)
(此时1是根)
然后就是推到状态看题解
我们用$f[i][j]$表示在$i$的子树中距离$i$的长度为$j$的点有多少个，那么显然，$f[i][j] = \sum f[t][j-1]$。
另$g[i][j]$为在以$i$为根的子树中，$x$,$y$ 到其$LCA(x,y)$的距离为$d$，$i$到$LCA(x,y)$的距离为$d-i$的这样的点对$(x,y)$有多少对。那么显然$g[i][j] = \sum g[t][j+1]$关于为什么$g$是这样转移，我们可以用下图解释
图中，g[2][0] 表示的点有2个，那么￥g[2][0] = 2￥，那么因为$2->1=1$，所以$1$号点的状态就是$g[1][d-(j-1)]=g[1][d-j+1]$(向上挪了一步，所以距离要减1）。
所以他是这么转移的。
好，现在我们考虑如何统计答案。
对于一个点$i$显然。$g[i][0]$就是答案的一部分，因为此时$i$已经是LCA了。然后我们新加入一个子节点是，对答案的贡献通过乘法原理可以计算的到是$g[i][j]*f[t][j-1]$至于为什么，可以看一下下面这个图
一下子就明白了，6 2 3 构成3个符合条件的的hotel。，我们发现如果可以从子树中把f和j继承过来就好了，然后跑一波长链剖分。(如果不会可以看这篇博客，如果不会指针，可以看zxyoi神仙的博客)
注意一下代码细节
# include <iostream>
# include <cstring>
# include <cstdio>
# include <vector>
# define int long long
using namespace std;
const int MAXN = 300100;
int len[MAXN],lson[MAXN];
struct edge{
int t,w,next;
}edges[MAXN<<2];
int head[MAXN];
int top;
void add(int f,int t,int w = 0) {
edges[++top].next = head[f];
edges[top].t = t;
edges[top].w = w;
head[f] = top;
}
int n,q;
void dfs1(int x,int fa){
for(int i = head[x];i;i = edges[i].next){
int t = edges[i].t;
if(t==fa)continue;
dfs1(t,x);
if(len[t]>len[lson[x]])lson[x] = t;
}
len[x] = len[lson[x]]+1;
}
long long tmp[MAXN<<2],*f[MAXN],*g[MAXN],*id = tmp;
long long ans;
void work(int x,int fa){
if(lson[x])f[lson[x]] = f[x]+1,g[lson[x]] = g[x]-1,work(lson[x],x);
f[x][0] = 1;ans+=g[x][0];
for(int i = head[x];i;i = edges[i].next){
int t = edges[i].t;
if(t==fa||to==lson[x])continue;
f[t] = id;id+=len[t]<<1;
g[t] = id;id+=len[t]<<1;
work(t,x);
for( int j = 0; j < len[t]; j++){//处理答案
if(j) ans += f[x][j - 1] * g[t][j];
ans += g[x][j + 1] * f[t][j];//为了处理三个点均是x的子节点和1个不是x的子节点的情况。不可能2个都不是x的子节点，因为这是一棵树
}
for( int j = 0; j < len[t]; j++){//处理转移
g[x][j + 1] += f[x][j + 1] * f[t][j];
if(j) g[x][j - 1] += g[t][j];
f[x][j + 1] += f[t][j];
}
}
}
signed main(){
scanf("%lld",&n);
int fr,t;
for(int i = 1;i<n;i++){
scanf("%lld%lld",&fr,&t);add(fr,t);add(t,fr);
}
dfs1(1,0);
f[1] = id,id+=len[1]<<1;
g[1] = id;id+=len[1]<<1;
work(1,0);
printf("%lld",ans);
return 0;
}
){kind=link}