卡特兰数

通项公式： 1:$f(n) = \frac{C_{2n}^n}{n+1}$ 2:$f(n) = \sum\limits_{i=0}^{n-1}f(i)*f(n-i-1)$ 常用变形3:$f(n) = C_{2n}^{n}-C_{2n}^{n-1}$ 4.$h(n)=h(n-1)*\frac{(4*n-2)}{(n+1)}$

应用

有一个长度为$2n$的01序列，其中1,0各$n$个，要求对于任意的整数$k∈[1,n] k \in [1,n]$数列的前$k$个数中，1的个数不少于0。

我们把01操作看成是在平面直角坐标系中行走，1向右上走，0向左下走最后一定走到了$(2n,0)$如图 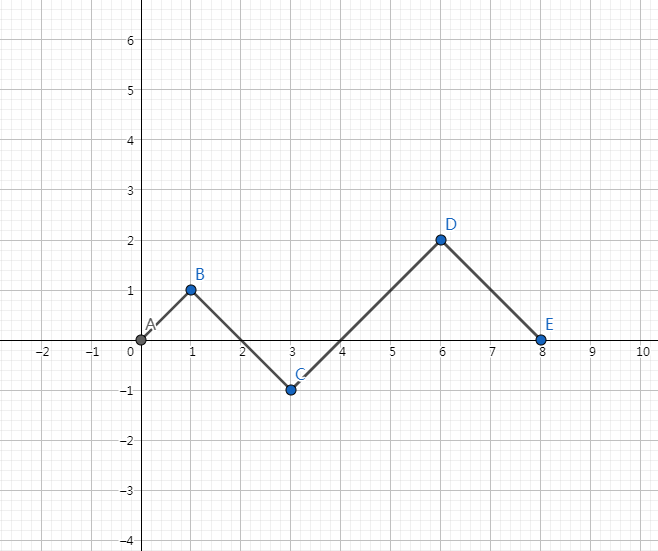那么路径的数量就是在$2n$步中选择$n$步，结果是$C_{2n}^n$，然后加入一个限制条件，对于：对于任意前缀，1的个数不少于0。 那么转化到坐标系中，也就是说走的路径不应该穿过x轴，即直线$ y=0$，也就是不接触$y=-1$。 于是我们把与$y=−1$的接触点的右边整条路径以$y=−1$为对称轴翻折，于是终点变为了$(2n,−2)$。如下图： 那么此时，从$(0,0)$到$(2n,−2)$的路径必定至少穿过一次$y=−1$，不满足条件，那么此时的路径数量即为总路径数中不符合题意的路径数，那么我们用总路径数减去不符合的路径数，就是最终的答案。 而此时的路径数量也很简单，由于反转后终点向下移了两位，也就意味着$ n-1$步是1，$n+1$步是0，总方案$C_{2n}^{n-1}$，那么最终的答案就是$C_{2n}^{n}-C_{2n}^{n-1}$

诶，这不就是卡特兰数吗。

卡特兰数应用

1、出栈次序：一个栈（无穷大）的进栈次序为1、2、3……n。不同的出栈次序有几种。 我们可以这样想，假设k是最后一个出栈的数。比k早进栈且早出栈的有k-1个数，一共有h(k-1)种方案。比k晚进栈且早出栈的有n-k个数，一共有h(n-k)种方案。所以一共有h(k-1)h(n-k)种方案。显而易见，k取不同值时，产生的出栈序列是相互独立的，所以结果可以累加。k的取值范围为1至n，所以结果就为h(n)= h(0)h(n-1)+h(1)h(n-2) + … + h(n-1)h(0)。 出栈入栈问题有许多的变种，比如n个人拿5元、n个人拿10元买物品，物品5元，老板没零钱。问有几种排队方式。熟悉栈的同学很容易就能把这个问题转换为栈。值得注意的是，由于每个拿5元的人排队的次序不是固定的，所以最后求得的答案要n!。拿10元的人同理，所以还要n!。所以这种变种的最后答案为h(n)n!*n!。

 2、二叉树构成问题。有n个结点，问总共能构成几种不同的二叉树。
        我们可以假设，如果采用中序遍历的话，根结点第k个被访问到，则根结点的左子树有k-1个点、根结点的右指数有n-k个点。k的取值范围为1到n。讲到这里就很明显看得出是卡特兰数了。这道题出现在2015年腾讯实习生的在线笔试题中。有参加过的同学想必都有印象。
  
 3、凸多边形的三角形划分。一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案。
         这也是非常经典的一道题。我们可以这样来看，选择一个基边，显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p1pn，我们就可以用p1、pn和另外一个点假设为pi做一个三角形，并将多边形分成三部分，除了中间的三角形之外，一边是i边形，另一边是n-i+1边形。i的取值范围是2到n-1。所以本题的解c(n)=c(2)*c(n-1)+c(3)*c(n-2)+...c(n-1)*c(2)。令t(i)=c(i+2)。则t(i)=t(0)*t(i-1)+t(1)*t(i-2)...+t(i-1)*t(0)。很明显，这就是一个卡特兰数了。
        
    4、其他。诸如括号匹配问题、01序列问题、n边形格子从左下角走到右上角不跨过对角线问题。这些都是卡特兰数，其他问题也基本上是上面问题的变种。证明过程就不再赘述了。

两类斯特林数

第一类斯特林数

意义：$\begin{bmatrix}n\\m\end{bmatrix}$表示$n$元素分成$m$个环的方案数 $\begin{bmatrix}n\\m \end{bmatrix} = \begin{bmatrix}n-1\\m-1\end{bmatrix}+(n-1) * \begin{bmatrix} n-1\\m \end{bmatrix}$ 理解：考虑从$n−1$个元素推过来，如果两个空环肯定是不符合的空一个环则单独成环，如果$n−1$的时候就没有空环就任意放在一个元素前 性质\(n! = \sum\limits_{i = 0}^{n}\begin{bmatrix}n\\i\end{bmatrix}\)

第二类斯特林数

$\begin{Bmatrix} n\\m\end{Bmatrix}$表示$n$个有区别的小球丢进$m$个无区别的盒子的方案数。 计算： \(\begin{Bmatrix}n\\m\end{Bmatrix}=\begin{Bmatrix}n-1\\m-1\end{Bmatrix}+m*\begin{Bmatrix}n-1\\m\end{Bmatrix}\) 性质 $m^n=\sum\limits_{i=0}^{m}\begin{Bmatrix}n\\i\end{Bmatrix}*i!*C(m,i)$ 反正我觉得联赛也考不到这玩意，既然L喊看一下就了解一下吧。

注意

附上几组卡特兰数方便考试的时候快速反应过来 $f(1) = 1$ $f(2) = 2$ $f(3) = 5$ $f(4) = 14$ $f(5) = 42$ $f(6) = 132$