题面
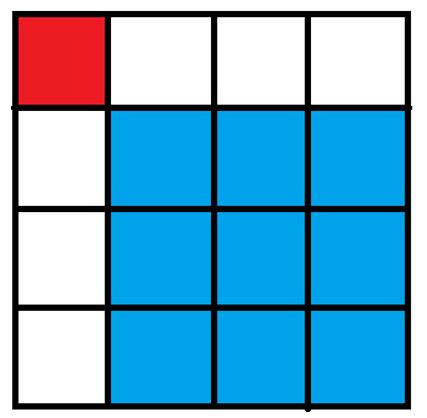
有一个无限大的矩形,初始时你在左上角(即第一行第一列),每次你都可以选择一个右下方格子,并瞬移过去(如从下图中的红色格子能直接瞬移到蓝色格子),求到第n行第m列的格子有几种方案,答案对1000000007取模。
Input
多组测试数据。
两个整数n,m(2≤n,m≤100000)
Output
一个整数表示答案
Sample Input
4 5
Sample Output
10
解答
一道组合数学的题,考虑枚举步数,然后计算。考虑竖着,一共有n行,需要花n-1步,然后在每一步之间插个板,一共可以插入n-2个板子,所以答案就是\(n-2 \choose i-1\)
同样的对于m列也可以这么考虑,那么答案就是\(m-2\choose i-1\)
所以统计总的答案就是\(\sum\limits_{i=1}^{n-1}{n-2\choose i-1}\times {m-2\choose i-1}\)
当然也可以化简为我不知道这么化出来的
\(m+n-4\choose n-2\)
现行处理阶乘和阶乘逆元。$O(1)$计算组合数就好了。代码:
# include <iostream>
# include <cstring>
# include <cstdio>
# define int long long
using namespace std;
const int MAXN = (int)2e5+10;
const int mod = 1000000007;
int fac[MAXN],rev[MAXN];
int n,m;
int fp(int b,int p){
int ans = 1;
while(p){
if(p&1)ans = ans*b%mod;
b = b*b%mod;
p>>=1;
}
return ans;
}
void init(){
fac[0] = 1;
for(int i = 1;i<MAXN;i++)fac[i] = fac[i-1]*i%mod;
rev[MAXN-1] = fp(fac[MAXN-1],mod-2);
for(int i = MAXN-2;i>=0;i--)rev[i] = (rev[i+1]*(i+1))%mod;
}
int C(int n,int m){return (fac[m]*rev[n]%mod)*rev[m-n]%mod;}
signed main(){
init();
int n,m;
while(scanf("%lld%lld",&n,&m)!=EOF){
long long ans = 0;
if(n>m)swap(n,m);
for(int i = 1;i<=n-1;i++)ans = (ans+C(i-1,n-2)*C(i-1,m-2))%mod;
printf("%lld\n",ans);
}
return 0;
}
