KMP基本思想

设主串（下文中称为A串）为：a b a a b a b

模式串（下文中称为B串）为：a b a b

（两个串的第一个下标都为1）

首先，若按照朴素算法，当发现A串与B串失配的时候，就会枚举A的下一位重新开始匹配，但是我们发现第1次匹配时前三位是成功匹配了的，若重新从第2位开始枚举就会浪费掉这些信息，我们考虑如何用这些信息来减少我们的匹配次数，从而优化时间复杂度

比如说上面的例子，若第1次失配后直接以A的第2位为起点，由于B[1]！=A[2]（B[1]为a而A[2]为b），此时A串与B串肯定也不匹配，我们考虑能不能直接跳过这些没有意义的匹配，观察第一次匹配成功了的三个字符（即a b a），第1位是等于第3位的，那我们就可以直接从A的第3位开始与B匹配，即此时应为： A a b a a b a b B a b a b 那我们不断地这样进行下去，就会省去很多不必要的匹配

那么问题来了，我们如何确定B从A的哪个位置开始继续匹配呢

于是这个时候我们的重头戏登场了

我们定义next[i]表示除去第i个字符，在从第1个字符到第（i-1）个字符组成的字符串中最长的相同前缀和后缀的长度。（比如说一个字符串abcab，那它最长的相同前缀和后缀的长度就为2，即为ab） 那么每当失配的时候，我们就把B的这一位移到这一位的next指向的那个位置，如下图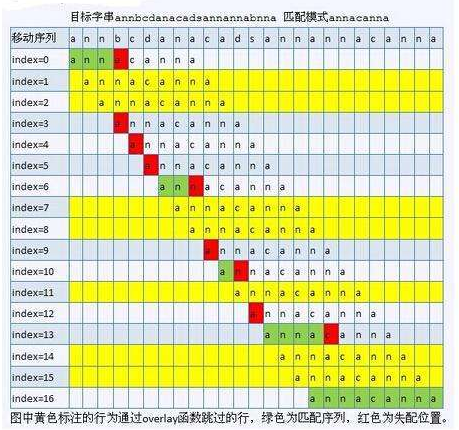： 这样的话，很多操作都被省去了，时间复杂度就会大大地得到优化

代码如下：

j=0;                                             //起初匹配了B的第0位 
for(i=1;i<=n;++i)                                //枚举A中的每一位 
{
	while(j&&A[i]!=B[j+1])  j=next[j];           //如果失配,则不断把B向右移,直到成功匹配 
	if(A[i]==B[j+1])  j++;                       //如果这一位是成功匹配了的,那j就移到下一位 
	if(j==m)                                     //如果成功匹配 
	{
		printf("%d\n",i-j+1);                    //输出成功匹配的第一位 
		j=next[j];                               //B继续向右移 
	}
}

next数组才是kmp的精髓

接下来就是求kmp next的关键 那么问题又来了，我们怎么确定next数组的值呢

因为next[i]记录的是B串中1到（i-1）中最长的前缀与后缀的重复长度，那我们不妨换一种角度，把求next数组看做是B自己与自己匹配

为什么呢？假设我们用B1，B2来代替主串和模式串，那么B1，B2肯定是全部相等的（都为B），那1到（i-1）的部分也肯定是相等的，那next[i]也可以表示成1到（i-1）中B2的前缀与B1的后缀相同的最长的重复长度

那就可以用刚才的方法来求next数组

j=0;                                             //起初匹配了B的第0位 
next[1]=0;                                       //第1位的next值为0 
for(i=2;i<=m;++i)                                //枚举B的每一位 
{
	while(j&&B[i]!=B[j+1])  j=next[j];           //如果失配,则不断把B向右移,直到成功匹配 
	if(B[i]==B[j+1])  j++;                       //如果这一位是成功匹配了的,那j就移到下一位 
	next[i]=j;                                   //此时i位置的next值就为j 
}

复杂度分析

在上文中已经提到KMP的时间复杂度为O（m+n），内层的while循环以及外层的for循环利用到了均摊思想，所以复杂度为O（m+n）

自己的笔记前面是抄的

指针i,j的含义是 A[i-j+1…i]与B[1…j]完全相等。 next数组表示匹配到B数组的第j个字母而第j+1个字母不能匹配了时候，新的j的最大值 其实就是一个自我匹配个过程，可以使用之前的next数组的数据来计算 假如我们已经匹配出next[1…i],现在求next[i+1].其实就是看B[next[i]+1]是否等于B[i+1],如果相等，那么next[i+1] = j,否则是p[p[i]]大概就是这个意思，应该能理解，实在不能就看上面的书.

实现见板子