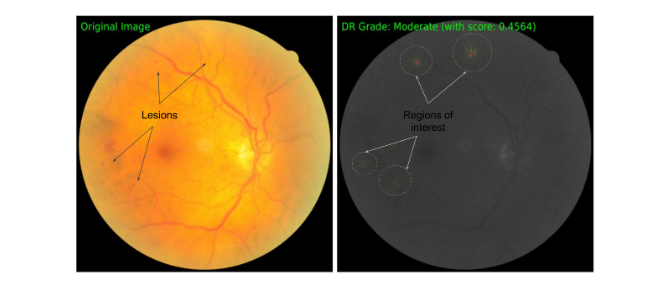
Axiomatic Attribution for Deep Networks

本文发表于2017年ICML会议。本文提出了一种叫做积分梯度的方法，满足敏感性（Sensitivity）和实现不变形（Implemention Invariance）。

• 敏感性: 一个归因方法的敏感性是指对于任意输入$x$和baseline $x’$而言，当$x$存在一处与$x’$不同的特征，那么基于$x’$对$x$的归因结果就应该被赋予一个非0的归因。

• 实现不变形：指对于不同实现的网络而言，若对于任意输入$x$，若他们的输出都是相同的，则称他们具备实现不变形。

文章认为对于一个归因方法而言，满足这两条性质非常重要。之前的方法，例如直接的梯度归因，并不同时满足这两条性质。

Method

积分梯度方法的基本思想是：给定一个baseline $x’$，得到一个网络的输出，然后对其进行变化，逐渐变成$x$，其中每向$x$走一步都可以得到一个结果（如下面的tom和jerry所示），计算这个结果对输入（就是$x$走到$x’$的中间临时结果）的导数，然后对导数进行积分就得到了。用公式描述就是

\(InteGrad(x)=(x-x')\times\int_{0}^1\frac{\partial F(x^{\prime}+\alpha\times(x-x^{\prime}))}{\partial x}d\alpha\)

但是存在一个问题：$x’$到$x$有许多条路径，那么选择哪一条呢？想象一下PPT里面的渐变过渡动画，过渡的方法有千千万万种，不同的路径可能会得到不同的结果。假设有$n$个特征，如过按照特征出现顺序来计算影响的话，就会有$n!$种可能得归因结果。（先在$x’$上添加$x$的第一个特征，计算一下梯度，在加第二个特征，再算一下以此类推）为了避免这个问题作者采用的方法是：把这些路径通通平均掉。就是如下图的绿色直线。这里有个疑问，这个直线就是平均结果感觉上是没问题的，但是能不能严格证明一下？

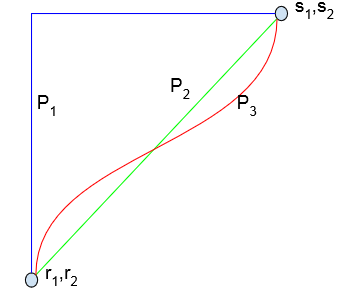
作者指出，这样的走直线的走法是唯一满足对称性的走法。所谓对称性就是把输入对称一下，输出结果也是对称的。证明短文中没提，有空看一下完整论文再来补坑吧

这样积分梯度方法就完了。为了方便计算，把积分改成求和，如下： \(InteGrad^{approximate}(x_i-x_i^{\prime})\times\Sigma_{k=1}^m\frac{\partial F(x^{\prime}+\frac km\times(x-x^{\prime}))}{\partial x_i}\times\frac1m\) 作者指出，$m$的取值通常在20-300就够了，作者建议检查归因结果是否近似地增加了$x$分数和$x’$的分数之间的差异（？没看懂他在说什么），否则增加$m$的值。

放两个结果图：