Introduction & Motivation & Background & Related Works
传统的卷积神经网络优化主要有两个方面:通过张量低秩分解来压缩核参数;通过设计如MobileNet之类的网络结构来优化。作者希望设计一种方法来综合二者。作者关注:1、张量方法——要么基于参数压缩来优化,要么基于计算量优化;2、基于neural architecture的优化,如深度可分离卷积。
Method
1、1x1卷积等价于张量与和参数在通道维度进行张量简并
tensor contraction: 张量缩并/张量缩约,即让张量降两阶。 张量n模积定义为$\mathcal{P}=\tau\times_{n}M=\mathcal{P}_{i_0,\cdots,i_N}=\sum\limits_{k=0}^{I_n}\tau_{i_0,\cdots,i_{n-1},k,i_{n+1},\cdots,i_N}M_{i_n,k}$,其中$\tau\in\mathcal{R}^{I_0\times I_1\times \cdots\times I_N},M\in R^{J\times I_n}$,两个张量进行简并说白了就是在某一维度上的纤维(fiber)都乘以矩阵M,$v\in R^{1,i_n},M\in R^{i_n,k},vM\in R^{1,k}$。
然后就能发现,1x1卷积就是一种张量n模积,有如下形式
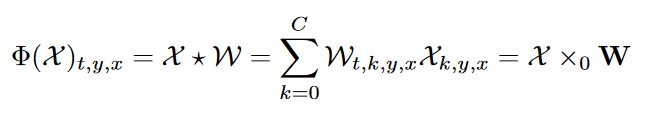
2、深度可分离卷积是对普通卷积的CP分解
对于卷积$\mathcal{F}=\mathcal{X}*\mathcal{W}$,有
\(\mathcal{F}_{t,y,x}=\sum\limits_{k=1}^{C}\sum\limits_{j=1}^{H}\sum\limits_{i=1}^{W}\mathcal{W}(t,k,j,i)\mathcal{X}(k,j+y,i+x)\)
对$\mathcal{W}(t,k,j,i)$进行CP分解,得到kruskal形式:
\(\mathcal{W}(t,k,j,i)=\sum\limits_{r=0}^{R-1}U^{(T)}_{t,r}U^{(C)}_{s,r}U^{(H)}_{j,r}U^{(W)}_{i,r}\)
然后带回去,得到:
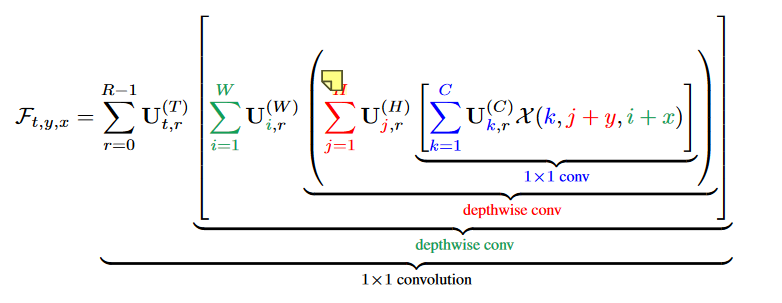
3、基于Tucker分解的卷积
按照Tucker分解方式,将核参数分解了,然后并入卷积式子,将Tucker核与空间维度的Kruskal形式的$U^{(H/W)}_{j/i,r}$进行简并。如文章所示:
 简化地写,就成了这样:
简化地写,就成了这样:
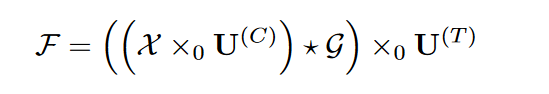
Factorized higher-order convolutions
对于高维张量,用Kruskal形式来表述参数,表述为$\mathcal{W}=[\lambda;U^{(T)};U^{(C)};U^{(K_0)}\cdots ;U^{(K_{N-1})}]$ 然后卷积可以写为: \(\Phi(\mathcal{X})_{t,i_0,i_1,\cdots,i_n}=\sum\limits_{r=0}^{R}\sum\limits_{s=0}^{C}\sum\limits_{i_0=0}^{K_0}\cdots\sum\limits_{i_{N-1}=0}^{K_{N-1 }} \lambda_r[U^{(T)}_{t,r}U^{(C)}_{s,r}U^{(K_0)}_{i_0,r}\cdots U_{i_{N-1 }} ^{K_{N-1 }} \mathcal{X}_{s,\cdots,i_{N-1 }} ]\)
调整一下乘积的顺序(前面的一堆$\sum$我就略过了),可以写成: \(\sum\cdots\sum\lambda_r[U^{(T)}\mathcal{X}_sU^{(C)}U^{(K_0)}\cdots U^{(k_{N-1})}]\) 然后定义一个$\rho(\mathcal{X})$操作为: \(\rho(\mathcal{X})=(\mathcal{X}\star_1U^{(K_0)}\cdots \star_{N+1}U^{(K_{N-1})})\) 说白了这个$\rho(\mathcal{X})$就是做超空间上的卷积。然后上面的那一坨可以写成: \(\mathcal{F}=\rho(\Phi(\mathcal{X}\times_0U^{(T)}))\times_0(diag(\lambda)U^{(C)})\) 这样优化的意义就在于把$N$维卷积参数量从$T\times C\times K_0\times K_1\cdots\times K_{N-1}$降低到了$T+C+\sum\limits_{i=0}^{N-1}I_k$ 要想将训练好的参数拓展一维,只需要把$\rho$换成$\hat{\rho}$就行,$\hat{\rho}$被定义为: \(\hat{\rho}(\mathcal{X})=\rho(\mathcal{X})\star_{N+1}U^{K_{N+1 }}\) 确实说白了就是他这个形式方便拓展维度,要拓展就多塞一项就行。



